spurious correlations
discover · random · spurious scholar
← previous page · next page →


View details about correlation #1,159



View details about correlation #2,470
What else correlates?
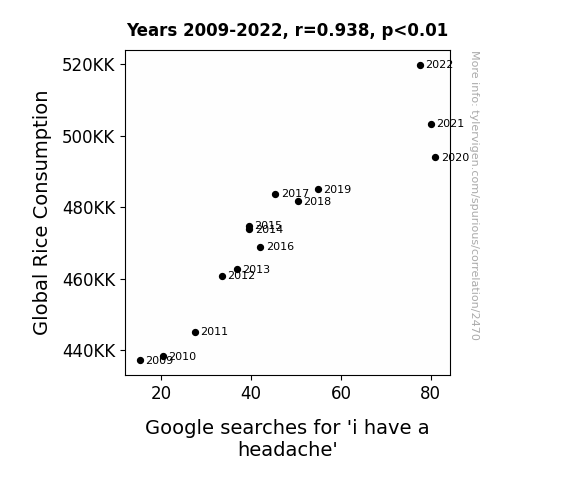
Global Rice Consumption · all food
Google searches for 'i have a headache' · all google searches
Global Rice Consumption · all food
Google searches for 'i have a headache' · all google searches


View details about correlation #4,253
What else correlates?
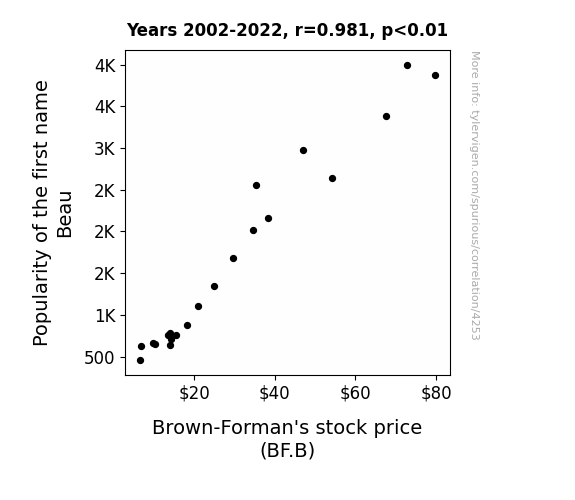
Popularity of the first name Beau · all first names
Brown-Forman's stock price (BF.B) · all stocks
Popularity of the first name Beau · all first names
Brown-Forman's stock price (BF.B) · all stocks


View details about correlation #2,317



View details about correlation #5,009
What else correlates?
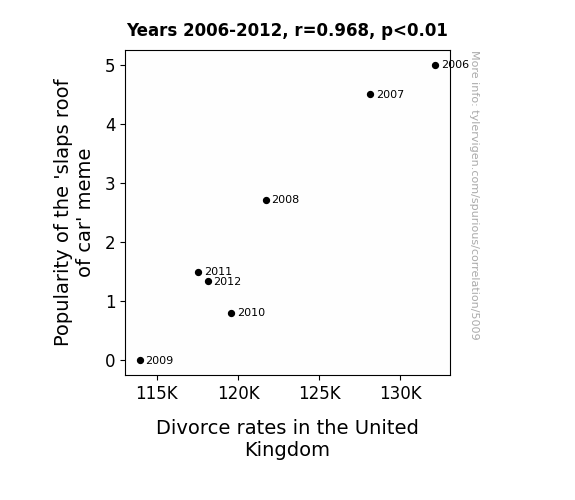
Popularity of the 'slaps roof of car' meme · all memes
Divorce rates in the United Kingdom · all weird & wacky
Popularity of the 'slaps roof of car' meme · all memes
Divorce rates in the United Kingdom · all weird & wacky


View details about correlation #3,384

What else correlates?
The number of Breweries in the United States · all food
Solar power generated in Peru · all energy
The number of Breweries in the United States · all food
Solar power generated in Peru · all energy


View details about correlation #2,724

What else correlates?
Bachelor's degrees awarded in Library science · all education
Ticket sales for Oakland Athletics games · all sports
Bachelor's degrees awarded in Library science · all education
Ticket sales for Oakland Athletics games · all sports


View details about correlation #1,622

What else correlates?
Dried manure used for fertilizer in the US · all weird & wacky
Customer satisfaction with Target · all weird & wacky
Dried manure used for fertilizer in the US · all weird & wacky
Customer satisfaction with Target · all weird & wacky


View details about correlation #2,285

What else correlates?
The number of transit police in Texas · all cccupations
Google searches for 'how to do magic' · all google searches
The number of transit police in Texas · all cccupations
Google searches for 'how to do magic' · all google searches


View details about correlation #2,697

What else correlates?
GMO use in corn grown in Michigan · all food
Enbridge's stock price (ENB) · all stocks
GMO use in corn grown in Michigan · all food
Enbridge's stock price (ENB) · all stocks


View details about correlation #1,874
What else correlates?
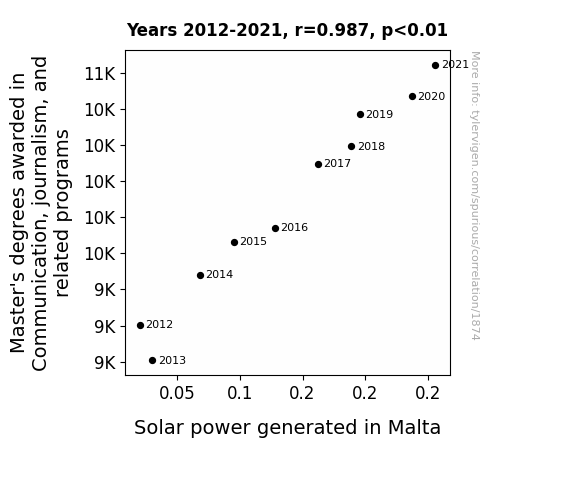
Master's degrees awarded in journalism · all education
Solar power generated in Malta · all energy
Master's degrees awarded in journalism · all education
Solar power generated in Malta · all energy


View details about correlation #4,241

What else correlates?
Popularity of the first name Sarah · all first names
Remaining Forest Cover in the Brazilian Amazon · all weird & wacky
Popularity of the first name Sarah · all first names
Remaining Forest Cover in the Brazilian Amazon · all weird & wacky


View details about correlation #5,895

What else correlates?
Google searches for 'matt levine' · all google searches
The number of college administrators in Ohio · all cccupations
Google searches for 'matt levine' · all google searches
The number of college administrators in Ohio · all cccupations


View details about correlation #2,401



View details about correlation #1,709
What else correlates?
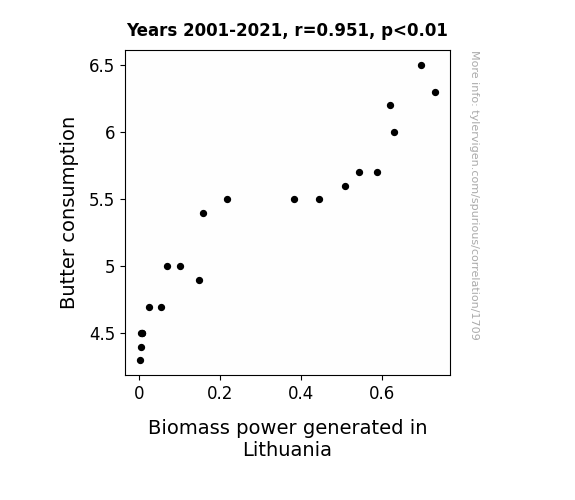
Butter consumption · all food
Biomass power generated in Lithuania · all energy
Butter consumption · all food
Biomass power generated in Lithuania · all energy


View details about correlation #2,596

What else correlates?
Popularity of the first name Tristen · all first names
Asthma attacks in American children · all weird & wacky
Popularity of the first name Tristen · all first names
Asthma attacks in American children · all weird & wacky


View details about correlation #5,142
What else correlates?
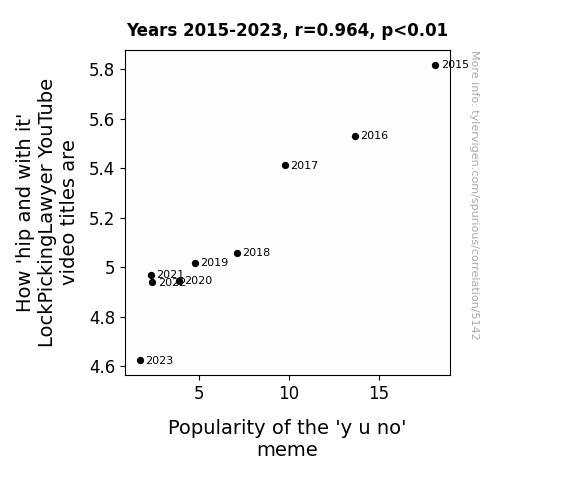
How 'hip and with it' LockPickingLawyer YouTube video titles are · all YouTube
Popularity of the 'y u no' meme · all memes
How 'hip and with it' LockPickingLawyer YouTube video titles are · all YouTube
Popularity of the 'y u no' meme · all memes


View details about correlation #2,906
What else correlates?
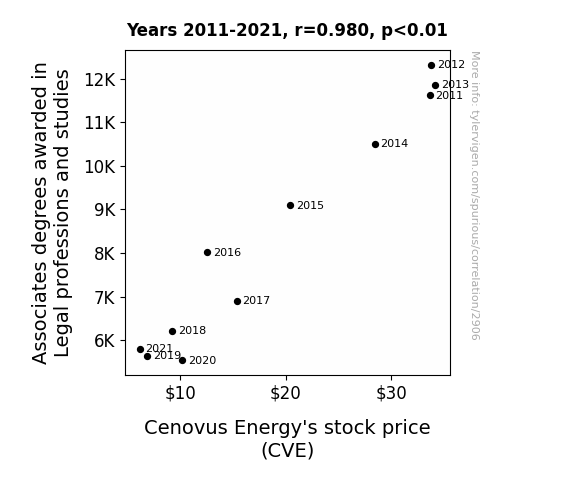
Associates degrees awarded in Legal professions and studies · all education
Cenovus Energy's stock price (CVE) · all stocks
Associates degrees awarded in Legal professions and studies · all education
Cenovus Energy's stock price (CVE) · all stocks
Why this works
- Data dredging: I have 25,237 variables in my database. I compare all these variables against each other to find ones that randomly match up. That's 636,906,169 correlation calculations! This is called “data dredging.”
Fun fact: the chart used on the wikipedia page to demonstrate data dredging is also from me. I've been being naughty with data since 2014.
Instead of starting with a hypothesis and testing it, I instead tossed a bunch of data in a blender to see what correlations would shake out. It’s a dangerous way to go about analysis, because any sufficiently large dataset will yield strong correlations completely at random. - Lack of causal connection: There is probably no direct connection between these variables, despite what the AI says above.
Because these pages are automatically generated, it's possible that the two variables you are viewing are in fact causually related. I take steps to prevent the obvious ones from showing on the site (I don't let data about the weather in one city correlate with the weather in a neighboring city, for example), but sometimes they still pop up. If they are related, cool! You found a loophole.
This is exacerbated by the fact that I used "Years" as the base variable. Lots of things happen in a year that are not related to each other! Most studies would use something like "one person" in stead of "one year" to be the "thing" studied. - Observations not independent: For many variables, sequential years are not independent of each other. You will often see trend-lines form. If a population of people is continuously doing something every day, there is no reason to think they would suddenly change how they are doing that thing on January 1. A naive p-value calculation does not take this into account.
You will calculate a lower chance of "randomly" achieving the result than represents reality.
To be more specific: p-value tests are probability values, where you are calculating the probability of achieving a result at least as extreme as you found completely by chance. When calculating a p-value, you need to assert how many "degrees of freedom" your variable has. I count each year (minus one) as a "degree of freedom," but this is misleading for continuous variables.
This kind of thing can creep up on you pretty easily when using p-values, which is why it's best to take it as "one of many" inputs that help you assess the results of your analysis.
- Y-axes doesn't start at zero: I truncated the Y-axes of the graphs above. I also used a line graph, which makes the visual connection stand out more than it deserves.
Nothing against line graphs. They are great at telling a story when you have linear data! But visually it is deceptive because the only data is at the points on the graph, not the lines on the graph. In between each point, the data could have been doing anything. Like going for a random walk by itself!
Mathematically what I showed is true, but it is intentionally misleading. If you click on any of the charts that abuse this, you can scroll down to see a version that starts at zero. - Confounding variable: Confounding variables (like global pandemics) will cause two variables to look connected when in fact a "sneaky third" variable is influencing both of them behind the scenes.
- Outliers: Some datasets here have outliers which drag up the correlation.
In concept, "outlier" just means "way different than the rest of your dataset." When calculating a correlation like this, they are particularly impactful because a single outlier can substantially increase your correlation.
Because this page is automatically generated, I don't know whether any of the charts displayed on it have outliers. I'm just a footnote. ¯\_(ツ)_/¯
I intentionally mishandeled outliers, which makes the correlation look extra strong. - Low n: There are not many data points included in some of these charts.
You can do analyses with low ns! But you shouldn't data dredge with a low n.
Even if the p-value is high, we should be suspicious of using so few datapoints in a correlation.
Pro-tip: click on any correlation to see:
- Detailed data sources
- Prompts for the AI-generated content
- Explanations of each of the calculations (correlation, p-value)
- Python code to calculate it yourself



