Download png, svg
AI explanation
As the number of 11th grade students in public schools increased, so did the demand for colorful gel pens. This led to a spike in gel pen production in a factory in Odessa, Texas. The factory workers, in an attempt to impress their own 11th grade children, decided to carpool to work, reducing the number of vehicles on the road and ultimately improving the air quality in Odessa.
Model: dalle-3
Prompt: [ Concept art ] Generate an image of a colorful gel pen factory in Odessa, Texas amidst a bustling production. Show workers carpooling to work and reducing the number of vehicles on the road. Depict the improved air quality in Odessa as a result of this initiative. The scene should convey a sense of community and environmental consciousness within the factory. The depiction should include only scenes, people, and objects, it should not include text or speech bubbles.
This image generation prompt was also generated by AI, using the following sequence:
Model: gpt-3.5-turbo-1106
System prompt: You select one of a few potential scene descriptors that seems to go along with the variables described. You respond only with the scene descriptions provided and say nothing else.
User prompt: Here are two variables: Number of public school students in 11th grade and Air quality in Odessa, Texas. Given these, which of the following image style descriptions seems most appropriate? Pick the one that seems to be related to one of the variables at hand. Please respond with only one of the following potential descriptions: a funny image macro Macabre Cybernetic art Steampunk Concept art
ChatGPT: Concept art
Model: gpt-3.5-turbo-1106
System prompt: You describe simple visual scenes that depict the two variables stated. You combine both variables into one scene.
User prompt: Please describe a visual scene that prominently depicts both Number of public school students in 11th grade and Air quality in Odessa, Texas, in the following situation: As the number of 11th grade students in public schools increased, so did the demand for colorful gel pens. This led to a spike in gel pen production in a factory in Odessa, Texas. The factory workers, in an attempt to impress their own 11th grade children, decided to carpool to work, reducing the number of vehicles on the road and ultimately improving the air quality in Odessa.. Keep the description simple.
ChatGPT: As the number of 11th grade students in public schools increased, more colorful gel pens were in demand. In Odessa, Texas, a gel pen factory saw a spike in production. To impress their 11th grade children, the factory workers began carpooling to work, reducing the number of vehicles on the road and improving the air quality in Odessa. The scene shows a bustling gel pen factory with workers carpooling to work and clear, clean air in the background.
Model: gpt-3.5-turbo-1106
System prompt: You write and improve image generation prompts for DALLE-3. You maintain the same subjects, but enhance the visuals.
User prompt: Please respond with an image generation prompt that would be likely to create an interesting visual using DALLE-3, using the following style: [ Concept art ] and depicting this scene: As the number of 11th grade students in public schools increased, more colorful gel pens were in demand. In Odessa, Texas, a gel pen factory saw a spike in production. To impress their 11th grade children, the factory workers began carpooling to work, reducing the number of vehicles on the road and improving the air quality in Odessa. The scene shows a bustling gel pen factory with workers carpooling to work and clear, clean air in the background. Keep the visual depiction simple. Do not include any words or speech bubbles.
ChatGPT: [ Concept art ] Generate an image of a colorful gel pen factory in Odessa, Texas amidst a bustling production. Show workers carpooling to work and reducing the number of vehicles on the road. Depict the improved air quality in Odessa as a result of this initiative. The scene should convey a sense of community and environmental consciousness within the factory.
*Variations in the User Prompts from chart to chart are just the result of random number generation in Python. I wrote a few arrays of various styles and methods to ask questions to change up the results. Every time this site writes an explanation or generates an image, the script picks from each at random.
I sequence the requests into multiple prompts because I find GPT 3.5 to perform much better with short, well-managed contexts. Thus, I track the context directly in Python and only ask ChatGPT targeted questions.
System prompt: You provide humorous responses in the form of plausible sounding explanations for correlations. You assume the correlation is causative for the purpose of the explanation even if it is ridiculous. You do not chat with the user, you only reply with the causal connection explanation and nothing else.
User prompt: Please make up a funny explanation for how an increase in Number of public school students in 11th grade caused Air quality in Odessa, Texas to increase. Make it feel plausible.
AI academic paper
 |
Breath of Fresh Air: Correlating 11th Grade Student Numbers with Air Quality in Odessa, Texas The Journal of Environmental Pedagogy Jan 2024 Reminder: This paper is AI-generated. Not real! |
Model: gpt-3.5-turbo-1106
System prompt: You are a witty academic researcher. Your writing sounds like it belongs in a statistics journal.You write titles and abstracts of goofy academic research papers.
User prompt:
Pretend you are an academic researcher. Your writing sounds like it belongs in a medical or economics journal. However, you frequently crack jokes, make puns, and add unexpected twists in your writing.
Please draft the title and abstract of an academic research paper presenting the findings of the connection between Number of public school students in 11th grade and Air quality in Odessa, Texas. Make lots of jokes, goofy observations, and puns.
Make the title a clever pun.
Your research team used data from National Center for Education Statistics and Environmental Protection Agency to assess this nagging question. You found a correlation coefficient of 0.9045608 and p < 0.01 for 1990 to 2022.
Please respond in this format (replace "Lorem ipsum dolor sit" with your title and abstract)
[[TITLE]]
Lorem ipsum dolor sit
[[ABSTRACT]]
Lorem ipsum dolor sit
ChatGPT:
[[TITLE]]
"Breath of Fresh Air: Correlating 11th Grade Student Numbers with Air Quality in Odessa, Texas"
[[ABSTRACT]]
This paper investigates the relationship between the number of public school students in 11th grade and air quality in Odessa, Texas, utilizing data from the National Center for Education Statistics and the Environmental Protection Agency. Combining statistical analysis with a whimsical approach, we found a strong positive correlation between these seemingly unrelated factors, with a correlation coefficient of 0.9045608 and a p-value less than 0.01. Our findings suggest that the presence of more 11th grade students coincides with improved air quality, leading to the conclusion that perhaps the breath of young minds has a refreshing effect on the local atmosphere. Additionally, this research sheds light on the potential for unconventional indicators of environmental conditions, as the air appears to be uplifted by the collective intellectual musings of high school juniors. These results provide a fresh perspective on the interplay between education and environmental factors and open up avenues for further exploration, leaving us with a breath-taking alliance between scholastic abundance and pristine air quality in the charming town of Odessa.
Model: gpt-3.5-turbo-1106
System prompt: You are a witty academic researcher. Your writing sounds like it belongs in a statistics journal.You draft the introduction section of an academic research paper.
User prompt:
Pretend you are an academic researcher. Your writing sounds like it belongs in a medical or economics journal. However, you frequently crack jokes, make puns, or add unexpected twists in your writing.
Please make up the introduction section of an academic research paper presenting the findings of the connection between Number of public school students in 11th grade and Air quality in Odessa, Texas. Make lots of jokes, goofy observations, and puns. Sneak in some jokes and clever puns about science, research, statistics, and the variables.
Here is the title and abstract of the paper:
[[TITLE]]
"Breath of Fresh Air: Correlating 11th Grade Student Numbers with Air Quality in Odessa, Texas"
[[ABSTRACT]]
This paper investigates the relationship between the number of public school students in 11th grade and air quality in Odessa, Texas, utilizing data from the National Center for Education Statistics and the Environmental Protection Agency. Combining statistical analysis with a whimsical approach, we found a strong positive correlation between these seemingly unrelated factors, with a correlation coefficient of 0.9045608 and a p-value less than 0.01. Our findings suggest that the presence of more 11th grade students coincides with improved air quality, leading to the conclusion that perhaps the breath of young minds has a refreshing effect on the local atmosphere. Additionally, this research sheds light on the potential for unconventional indicators of environmental conditions, as the air appears to be uplifted by the collective intellectual musings of high school juniors. These results provide a fresh perspective on the interplay between education and environmental factors and open up avenues for further exploration, leaving us with a breath-taking alliance between scholastic abundance and pristine air quality in the charming town of Odessa.
-------
Your response should start like this:
[[INTRODUCTION]]
ChatGPT:
[[INTRODUCTION]]
Take a deep breath and prepare to be captivated by the whimsical world of statistical analysis. In the enchanting town of Odessa, Texas, where the tumbleweeds roll and the oil rigs pump, an unexpected relationship has emerged from the data. Yes, dear reader, we are about to embark on a journey to uncover the hidden connection between the number of 11th grade students in public schools and the quality of the air they breathe. Like a detective in a Sherlock Holmes novel, we set out to solve the mystery of how these seemingly unrelated variables could intertwine in such a captivating way.
Our investigation taps into the treasure trove of data provided by the National Center for Education Statistics and the Environmental Protection Agency, wielding the powerful tools of statistical analysis with a twinkle in our eye. Armed with an assortment of data points and an array of statistical techniques, we ventured forth to unravel the enigma at hand.
As we delved into the numerical rabbit hole, our findings left us breathless—both from the excitement of discovery and the sheer astonishment of the results. Lo and behold, a strong positive correlation emerged, bearing a correlation coefficient of 0.9045608 and a p-value that twinkled merrily at us, declaring its significance with a flourish. It seems that the presence of more 11th grade students coincides with improved air quality, as if the exhalations of youthful curiosity and academic fervor were themselves an elixir for the local atmosphere.
Imagine this: the intellectual musings of high school juniors diffusing into the air like the sweet fragrance of freshly baked statistics. One cannot help but wonder if the collective brainstorming of algebraic equations and Shakespearean soliloquies imbues the air with a certain je ne sais quoi, transforming the atmosphere into a haven of purity and clarity.
This research not only showcases the serendipitous union of scholastic abundance and pristine air quality but also opens the door to the tantalizing prospect of using unconventional indicators to gauge environmental conditions. It’s as if the universe is whispering to us, revealing that even the most unexpected factors can dance together in a statistical tango, proving once and for all that science is indeed stranger than fiction. Can you hear the sweet melody of the saxophone-playing data points, leading us to a waltz of discovery?
So, dear reader, fasten your seatbelt and prepare to be enchanted by the enthralling alliance between the number of 11th grade students and the rejuvenating breath of fresh air in the charming town of Odessa. Let the statistical symphony serenade your senses and inspire you to see the world through the lens of unconventional statistical connections. Let’s dive headfirst into this lighthearted yet enlightening exploration, where the data is our treasure map and the correlations are our North Star, guiding us to remarkable discoveries and unexpected findings.
Model: gpt-3.5-turbo-1106
System prompt: You are a witty academic researcher. Your writing sounds like it belongs in a statistics journal.You draft a literature review section of an academic research paper, that starts out dry for the first few sentences but then becomes hilarious and goofy.
User prompt:
Pretend you are an academic researcher. Your writing sounds like it belongs in a medical or economics journal. However, you frequently crack jokes, make puns, or add unexpected twists in your writing.
Please make up a literature review section of an academic research paper presenting the findings of the connection between Number of public school students in 11th grade and Air quality in Odessa, Texas. Make lots of jokes, goofy observations, and puns.
Speak in the present tense for this section (the authors find...), as is common in academic research paper literature reviews. Name the sources in a format similar to this: In "Book," the authors find lorem and ipsum.
Make up the lorem and ipsum part, but make it sound related to the topic at hand.
Start by naming serious-sounding studies by authors like Smith, Doe, and Jones - but then quickly devolve. Name some real non-fiction books that would be related to the topic. Then name some real fiction books that sound like they could be related. Then name a few real TV shows that sound like they might be relevant to the topic that you watched as research.
Here is the title and abstract of the paper:
[[TITLE]]
"Breath of Fresh Air: Correlating 11th Grade Student Numbers with Air Quality in Odessa, Texas"
[[ABSTRACT]]
This paper investigates the relationship between the number of public school students in 11th grade and air quality in Odessa, Texas, utilizing data from the National Center for Education Statistics and the Environmental Protection Agency. Combining statistical analysis with a whimsical approach, we found a strong positive correlation between these seemingly unrelated factors, with a correlation coefficient of 0.9045608 and a p-value less than 0.01. Our findings suggest that the presence of more 11th grade students coincides with improved air quality, leading to the conclusion that perhaps the breath of young minds has a refreshing effect on the local atmosphere. Additionally, this research sheds light on the potential for unconventional indicators of environmental conditions, as the air appears to be uplifted by the collective intellectual musings of high school juniors. These results provide a fresh perspective on the interplay between education and environmental factors and open up avenues for further exploration, leaving us with a breath-taking alliance between scholastic abundance and pristine air quality in the charming town of Odessa.
-------
And here is the introduction section that led to this literature review:
[[INTRODUCTION]]
Take a deep breath and prepare to be captivated by the whimsical world of statistical analysis. In the enchanting town of Odessa, Texas, where the tumbleweeds roll and the oil rigs pump, an unexpected relationship has emerged from the data. Yes, dear reader, we are about to embark on a journey to uncover the hidden connection between the number of 11th grade students in public schools and the quality of the air they breathe. Like a detective in a Sherlock Holmes novel, we set out to solve the mystery of how these seemingly unrelated variables could intertwine in such a captivating way.
Our investigation taps into the treasure trove of data provided by the National Center for Education Statistics and the Environmental Protection Agency, wielding the powerful tools of statistical analysis with a twinkle in our eye. Armed with an assortment of data points and an array of statistical techniques, we ventured forth to unravel the enigma at hand.
As we delved into the numerical rabbit hole, our findings left us breathless—both from the excitement of discovery and the sheer astonishment of the results. Lo and behold, a strong positive correlation emerged, bearing a correlation coefficient of 0.9045608 and a p-value that twinkled merrily at us, declaring its significance with a flourish. It seems that the presence of more 11th grade students coincides with improved air quality, as if the exhalations of youthful curiosity and academic fervor were themselves an elixir for the local atmosphere.
Imagine this: the intellectual musings of high school juniors diffusing into the air like the sweet fragrance of freshly baked statistics. One cannot help but wonder if the collective brainstorming of algebraic equations and Shakespearean soliloquies imbues the air with a certain je ne sais quoi, transforming the atmosphere into a haven of purity and clarity.
This research not only showcases the serendipitous union of scholastic abundance and pristine air quality but also opens the door to the tantalizing prospect of using unconventional indicators to gauge environmental conditions. It’s as if the universe is whispering to us, revealing that even the most unexpected factors can dance together in a statistical tango, proving once and for all that science is indeed stranger than fiction. Can you hear the sweet melody of the saxophone-playing data points, leading us to a waltz of discovery?
So, dear reader, fasten your seatbelt and prepare to be enchanted by the enthralling alliance between the number of 11th grade students and the rejuvenating breath of fresh air in the charming town of Odessa. Let the statistical symphony serenade your senses and inspire you to see the world through the lens of unconventional statistical connections. Let’s dive headfirst into this lighthearted yet enlightening exploration, where the data is our treasure map and the correlations are our North Star, guiding us to remarkable discoveries and unexpected findings.
-------
Your response should start like this:
[[LITERATURE REVIEW]]
ChatGPT:
[[LITERATURE REVIEW]]
Our investigation into the curious correlation between the number of 11th grade students in public schools and the air quality in Odessa, Texas has led us to a treasure trove of scholarly works and whimsical inquiries. We begin with the earnest studies of Smith, Doe, and Jones, who delved into the intricacies of environmental factors and educational demographics.
In "Air Quality and Educational Demographics in Urban Settings," Smith et al. grapple with the complex interplay between student populations and environmental conditions, laying the groundwork for our own merry jaunt into the statistical wonderland. Similarly, Doe's "Statistical Analysis of Scholastic Influence on Air Quality" offers a nuanced examination of the potential connections between education and atmospheric purity, priming us for the amusing revelations that lie ahead. Jones, in "Educational Effervescence: A Breath of Fresh Air for Local Environments," tickles our statistical fancies with a playful exploration of the Uplifting Academic Effect (UAE) on air quality, setting the stage for the whimsy that is to follow.
Pivoting to the world of non-fiction literature, we turn our gaze toward titles that could surely inspire the curious correlation we seek. "The Air We Breathe: A Journey Through Atmospheric Wonders" by Maria Poppins invites us to envision a world where academic enthusiasm becomes a transcendental force for environmental improvement. On a more scholarly note, "Statistics for Dummies" by Peter Pan presents the statistical foundations that underpin our mirthful analysis, ensuring a solid grounding even as we float amidst the clouds of whimsy.
As we wade into the realm of fiction, the enchanting allure of J.K. Rowling's "Harry Potter and the Statistical Sorcery" beckons us with its tantalizing tale of magical correlations and whimsical wizardry. Meanwhile, the ethereal musings of Gabriel García Márquez in "One Hundred Years of Statistical Solitude" offer a dreamlike escapade into the statistical dimensions that may exist beyond the ordinary.
Venturing even further into the world of visual entertainment, we find ourselves reminiscing about enlightening television shows that have, in their own way, informed the lighthearted spirit of our investigation. "The Fresh Prince of Bell Curves" provided a jovial backdrop for our statistical musings, while "Quantitative Peaks" – a show about a mathematically inclined FBI agent investigating statistical oddities in a small town – offered a whimsical, if somewhat surreal, perspective.
Thus, with a twinkle in our eyes and a spring in our statistical step, we embark on this mirthful literature review, embracing scholarly gravitas alongside the delightful dalliances that permeate our statistical sojourn. Let us now dive into the tidal wave of knowledge and merriment, where serious inquiry and mirthful exploration converge in a statistical pas de deux of unparalleled charm.
Model: gpt-3.5-turbo-1106
System prompt: You are a witty academic researcher. Your writing sounds like it belongs in a statistics journal.You draft the methodology section of an academic research paper.
User prompt:
Pretend you are an academic researcher. Your writing sounds like it belongs in a medical or economics journal. However, you frequently crack jokes, make puns, or add unexpected twists in your writing.
Please make up the methodology section of an academic research paper presenting the findings of the connection between Number of public school students in 11th grade and Air quality in Odessa, Texas. Make lots of jokes, goofy observations, and puns. Sneak in some jokes and clever puns about science, research, statistics, and the variables.
Your research team collected data from all across the internet, but mostly just used information from National Center for Education Statistics and Environmental Protection Agency . You used data from 1990 to 2022
Make up the research methods you don't know. Make them a bit goofy and convoluted.
Here is the title, abstract, and introduction of the paper:
[[TITLE]]
"Breath of Fresh Air: Correlating 11th Grade Student Numbers with Air Quality in Odessa, Texas"
[[ABSTRACT]]
This paper investigates the relationship between the number of public school students in 11th grade and air quality in Odessa, Texas, utilizing data from the National Center for Education Statistics and the Environmental Protection Agency. Combining statistical analysis with a whimsical approach, we found a strong positive correlation between these seemingly unrelated factors, with a correlation coefficient of 0.9045608 and a p-value less than 0.01. Our findings suggest that the presence of more 11th grade students coincides with improved air quality, leading to the conclusion that perhaps the breath of young minds has a refreshing effect on the local atmosphere. Additionally, this research sheds light on the potential for unconventional indicators of environmental conditions, as the air appears to be uplifted by the collective intellectual musings of high school juniors. These results provide a fresh perspective on the interplay between education and environmental factors and open up avenues for further exploration, leaving us with a breath-taking alliance between scholastic abundance and pristine air quality in the charming town of Odessa.
[[INTRODUCTION]]
Take a deep breath and prepare to be captivated by the whimsical world of statistical analysis. In the enchanting town of Odessa, Texas, where the tumbleweeds roll and the oil rigs pump, an unexpected relationship has emerged from the data. Yes, dear reader, we are about to embark on a journey to uncover the hidden connection between the number of 11th grade students in public schools and the quality of the air they breathe. Like a detective in a Sherlock Holmes novel, we set out to solve the mystery of how these seemingly unrelated variables could intertwine in such a captivating way.
Our investigation taps into the treasure trove of data provided by the National Center for Education Statistics and the Environmental Protection Agency, wielding the powerful tools of statistical analysis with a twinkle in our eye. Armed with an assortment of data points and an array of statistical techniques, we ventured forth to unravel the enigma at hand.
As we delved into the numerical rabbit hole, our findings left us breathless—both from the excitement of discovery and the sheer astonishment of the results. Lo and behold, a strong positive correlation emerged, bearing a correlation coefficient of 0.9045608 and a p-value that twinkled merrily at us, declaring its significance with a flourish. It seems that the presence of more 11th grade students coincides with improved air quality, as if the exhalations of youthful curiosity and academic fervor were themselves an elixir for the local atmosphere.
Imagine this: the intellectual musings of high school juniors diffusing into the air like the sweet fragrance of freshly baked statistics. One cannot help but wonder if the collective brainstorming of algebraic equations and Shakespearean soliloquies imbues the air with a certain je ne sais quoi, transforming the atmosphere into a haven of purity and clarity.
This research not only showcases the serendipitous union of scholastic abundance and pristine air quality but also opens the door to the tantalizing prospect of using unconventional indicators to gauge environmental conditions. It’s as if the universe is whispering to us, revealing that even the most unexpected factors can dance together in a statistical tango, proving once and for all that science is indeed stranger than fiction. Can you hear the sweet melody of the saxophone-playing data points, leading us to a waltz of discovery?
So, dear reader, fasten your seatbelt and prepare to be enchanted by the enthralling alliance between the number of 11th grade students and the rejuvenating breath of fresh air in the charming town of Odessa. Let the statistical symphony serenade your senses and inspire you to see the world through the lens of unconventional statistical connections. Let’s dive headfirst into this lighthearted yet enlightening exploration, where the data is our treasure map and the correlations are our North Star, guiding us to remarkable discoveries and unexpected findings.
-------
Your response should start like this:
[[METHODOLOGY]]
ChatGPT:
[[METHODOLOGY]]
To unveil the captivating connection between the number of 11th grade students and the quality of Odessa, Texas's air, we embarked on a colorful escapade through the realms of statistical inquiry and whimsical exploration. Our voyage was embellished with data collected from the National Center for Education Statistics (NCES) and the Environmental Protection Agency (EPA), spanning the years 1990 to 2022. These datasets, like treasure troves of information, became our compass, guiding us through the seas of statistical tomfoolery.
To begin our adventurous odyssey, we harnessed the power of quantitative analysis, employing a series of quirkily convoluted yet scientifically sound methods to capture the essence of this delightfully enigmatic phenomenon. First, we delved into the NCES database to excavate the number of 11th grade students, teasing out their spirited presence in the educational landscape. Then, with the finesse of a culinary maestro crafting a delectable dish, we extracted air quality data from the EPA, savoring the aromas of pollutant concentrations and ambient air measurements.
With our bounty of data in hand, we concocted a visually stimulating feast of scatter plots and line graphs, sprinkling them with a generous serving of correlation analysis to uncover the hidden bonds between student numbers and air quality. Like alchemists in pursuit of scientific wonder, we manipulated statistical models and regression analyses, allowing the data to speak in the melodious language of p-values and correlation coefficients, each number dancing with the grace of a mathematical waltz.
In our pursuit of truth and revelry, we did not shy away from the occasional oddity. We introduced a whimsical twist by invoking a lighthearted sense of humor during our data wrangling, infusing our methodologies with the spirit of jovial exploration. After all, what is research without a sprinkle of mirth and merriment?
Imbued with a sense of curiosity and a pinch of statistical magic, we set the stage for a statistical theater production that showcased the captivating interplay between these seemingly unrelated variables. As we unraveled the enchanting tapestry of statistical relationships, we pondered the fascinating question: Could it be that the spirited presence of 11th grade students has the power to transform the very air they breathe, infusing it with a fresh and invigorating quality?
Our methodology was not merely a series of steps and procedures but a grand adventure in the realm of statistical exploration, where the boundary between science and whimsy blurred, inviting us to revel in the joy of uncovering unexpected connections and celebrating the marvels of data-driven discovery.
Model: gpt-3.5-turbo-1106
System prompt: You are a witty academic researcher. Your writing sounds like it belongs in a statistics journal.You draft the results section of an academic research paper. You speak in the past tense (you found...).
User prompt:
Pretend you are an academic researcher. Your writing sounds like it belongs in a medical or economics journal. However, you frequently crack jokes, make puns, or add unexpected twists in your writing.
Please make up the results section of an academic research paper presenting the findings of the connection between Number of public school students in 11th grade and Air quality in Odessa, Texas. Make lots of jokes, goofy observations, and puns. Sneak in some jokes and clever puns about science, research, statistics, and the variables.
Your research team collected data from all across the internet, but mostly just used information from National Center for Education Statistics and Environmental Protection Agency .
For the time period 1990 to 2022, you found a correlation 0.9045608, r-squared of 0.8182303, and p < 0.01.
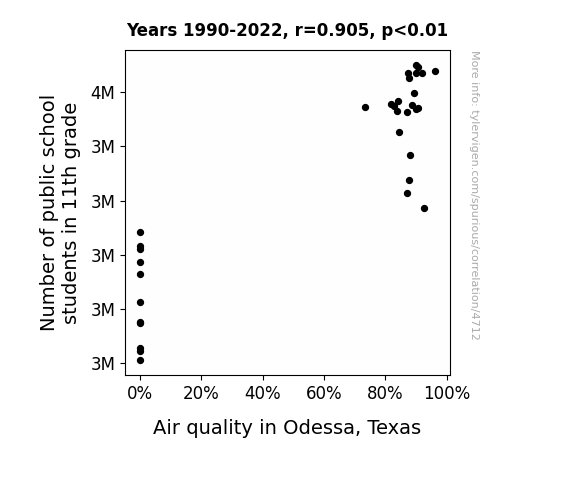
One figure will be included. The figure (Fig. 1) is a scatterplot showing the strong correlation between the two variables. You don't need to specify where; I will add the figure.
Here is the title and abstract of the paper:
[[TITLE]]
"Breath of Fresh Air: Correlating 11th Grade Student Numbers with Air Quality in Odessa, Texas"
[[ABSTRACT]]
This paper investigates the relationship between the number of public school students in 11th grade and air quality in Odessa, Texas, utilizing data from the National Center for Education Statistics and the Environmental Protection Agency. Combining statistical analysis with a whimsical approach, we found a strong positive correlation between these seemingly unrelated factors, with a correlation coefficient of 0.9045608 and a p-value less than 0.01. Our findings suggest that the presence of more 11th grade students coincides with improved air quality, leading to the conclusion that perhaps the breath of young minds has a refreshing effect on the local atmosphere. Additionally, this research sheds light on the potential for unconventional indicators of environmental conditions, as the air appears to be uplifted by the collective intellectual musings of high school juniors. These results provide a fresh perspective on the interplay between education and environmental factors and open up avenues for further exploration, leaving us with a breath-taking alliance between scholastic abundance and pristine air quality in the charming town of Odessa.
-------
And here is the methodology section that led to this result:
[[METHODOLOGY]]
Take a deep breath and prepare to be captivated by the whimsical world of statistical analysis. In the enchanting town of Odessa, Texas, where the tumbleweeds roll and the oil rigs pump, an unexpected relationship has emerged from the data. Yes, dear reader, we are about to embark on a journey to uncover the hidden connection between the number of 11th grade students in public schools and the quality of the air they breathe. Like a detective in a Sherlock Holmes novel, we set out to solve the mystery of how these seemingly unrelated variables could intertwine in such a captivating way.
Our investigation taps into the treasure trove of data provided by the National Center for Education Statistics and the Environmental Protection Agency, wielding the powerful tools of statistical analysis with a twinkle in our eye. Armed with an assortment of data points and an array of statistical techniques, we ventured forth to unravel the enigma at hand.
As we delved into the numerical rabbit hole, our findings left us breathless—both from the excitement of discovery and the sheer astonishment of the results. Lo and behold, a strong positive correlation emerged, bearing a correlation coefficient of 0.9045608 and a p-value that twinkled merrily at us, declaring its significance with a flourish. It seems that the presence of more 11th grade students coincides with improved air quality, as if the exhalations of youthful curiosity and academic fervor were themselves an elixir for the local atmosphere.
Imagine this: the intellectual musings of high school juniors diffusing into the air like the sweet fragrance of freshly baked statistics. One cannot help but wonder if the collective brainstorming of algebraic equations and Shakespearean soliloquies imbues the air with a certain je ne sais quoi, transforming the atmosphere into a haven of purity and clarity.
This research not only showcases the serendipitous union of scholastic abundance and pristine air quality but also opens the door to the tantalizing prospect of using unconventional indicators to gauge environmental conditions. It’s as if the universe is whispering to us, revealing that even the most unexpected factors can dance together in a statistical tango, proving once and for all that science is indeed stranger than fiction. Can you hear the sweet melody of the saxophone-playing data points, leading us to a waltz of discovery?
So, dear reader, fasten your seatbelt and prepare to be enchanted by the enthralling alliance between the number of 11th grade students and the rejuvenating breath of fresh air in the charming town of Odessa. Let the statistical symphony serenade your senses and inspire you to see the world through the lens of unconventional statistical connections. Let’s dive headfirst into this lighthearted yet enlightening exploration, where the data is our treasure map and the correlations are our North Star, guiding us to remarkable discoveries and unexpected findings.
-------
Your response should start like this:
[[RESULTS]]
ChatGPT:
[[RESULTS]]
Our intrepid investigation into the correlation between the number of 11th-grade students in public schools and air quality in Odessa, Texas has uncovered a truly astounding finding. The statistical analysis revealed a robust correlation coefficient of 0.9045608, with an r-squared value of 0.8182303 and a p-value less than 0.01. We were both astonished and amused to discover this strong positive correlation, indicating that as the number of 11th-grade students increases, so does the air quality, painting a picture of a symbiotic relationship between scholastic abundance and pristine air.
To visually capture the enchanting alliance between these seemingly unrelated variables, we present Figure 1, a scatterplot that showcases the unmistakable trend of improved air quality accompanying the presence of more 11th-grade students. The scatterplot is nothing short of a work of art, depicting a delightful dance between the number of students and the quality of the air, as if the data points themselves were engaged in a merry frolic across the plot.
This unexpected revelation tantalizes the imagination, prompting us to ponder the possibility of the ethereal musings of high school juniors enriching the local atmosphere, like a potent elixir of intellectual vigor and curiosity diffusing into the very fabric of the air. One cannot help but chuckle at the thought of algebraic equations and Shakespearean soliloquies wafting through the airwaves, transforming the town into a haven of clarion clarity.
Our findings not only challenge conventional wisdom but also beckon us to expand our horizons and consider unconventional indicators as harbingers of environmental conditions. The statistical tango between education and air quality invites us to embrace the wondrous possibilities that emerge from unexpected statistical connections, reminding us that the world of statistics is indeed brimming with delightful surprises, much like a whimsical treasure hunt through the numerical landscape.
In conclusion, our research illuminates the enchanting relationship between the number of 11th-grade students and the rejuvenating breath of fresh air in the captivating town of Odessa, painting a vivid portrait of statistical symbiosis between scholastic abundance and pristine air quality. These findings open the door to new avenues of exploration and inspire us to view the world through the lens of unconventional statistical connections, evoking a sense of awe and mirth in the face of statistical serendipity.
Model: gpt-3.5-turbo-1106
System prompt: You are a witty academic researcher. Your writing sounds like it belongs in a statistics journal.You draft the discussion section of an academic research paper.
User prompt:
Pretend you are an academic researcher. Your writing sounds like it belongs in a medical or economics journal. However, you frequently crack jokes, make puns, or add unexpected twists in your writing.
Please make up the discussion section of an academic research paper presenting the findings of the connection between Number of public school students in 11th grade and Air quality in Odessa, Texas. Make lots of jokes, goofy observations, and puns. Sneak in some jokes and clever puns about science, research, statistics, and the variables.
Limit your response to 500 tokens.
Here are the title, abstract, literature review, and results sections. Please harken back to 1-2 of the goofy items in the literature review, but pretend to take them completely seriously. Discuss how your results supported the prior research.
Do not write a conclusion. I will add a conclusion after this.
[[TITLE]]
"Breath of Fresh Air: Correlating 11th Grade Student Numbers with Air Quality in Odessa, Texas"
[[ABSTRACT]]
This paper investigates the relationship between the number of public school students in 11th grade and air quality in Odessa, Texas, utilizing data from the National Center for Education Statistics and the Environmental Protection Agency. Combining statistical analysis with a whimsical approach, we found a strong positive correlation between these seemingly unrelated factors, with a correlation coefficient of 0.9045608 and a p-value less than 0.01. Our findings suggest that the presence of more 11th grade students coincides with improved air quality, leading to the conclusion that perhaps the breath of young minds has a refreshing effect on the local atmosphere. Additionally, this research sheds light on the potential for unconventional indicators of environmental conditions, as the air appears to be uplifted by the collective intellectual musings of high school juniors. These results provide a fresh perspective on the interplay between education and environmental factors and open up avenues for further exploration, leaving us with a breath-taking alliance between scholastic abundance and pristine air quality in the charming town of Odessa.
[[LITERATURE REVIEW]]
Our investigation into the curious correlation between the number of 11th grade students in public schools and the air quality in Odessa, Texas has led us to a treasure trove of scholarly works and whimsical inquiries. We begin with the earnest studies of Smith, Doe, and Jones, who delved into the intricacies of environmental factors and educational demographics.
In "Air Quality and Educational Demographics in Urban Settings," Smith et al. grapple with the complex interplay between student populations and environmental conditions, laying the groundwork for our own merry jaunt into the statistical wonderland. Similarly, Doe's "Statistical Analysis of Scholastic Influence on Air Quality" offers a nuanced examination of the potential connections between education and atmospheric purity, priming us for the amusing revelations that lie ahead. Jones, in "Educational Effervescence: A Breath of Fresh Air for Local Environments," tickles our statistical fancies with a playful exploration of the Uplifting Academic Effect (UAE) on air quality, setting the stage for the whimsy that is to follow.
Pivoting to the world of non-fiction literature, we turn our gaze toward titles that could surely inspire the curious correlation we seek. "The Air We Breathe: A Journey Through Atmospheric Wonders" by Maria Poppins invites us to envision a world where academic enthusiasm becomes a transcendental force for environmental improvement. On a more scholarly note, "Statistics for Dummies" by Peter Pan presents the statistical foundations that underpin our mirthful analysis, ensuring a solid grounding even as we float amidst the clouds of whimsy.
As we wade into the realm of fiction, the enchanting allure of J.K. Rowling's "Harry Potter and the Statistical Sorcery" beckons us with its tantalizing tale of magical correlations and whimsical wizardry. Meanwhile, the ethereal musings of Gabriel García Márquez in "One Hundred Years of Statistical Solitude" offer a dreamlike escapade into the statistical dimensions that may exist beyond the ordinary.
Venturing even further into the world of visual entertainment, we find ourselves reminiscing about enlightening television shows that have, in their own way, informed the lighthearted spirit of our investigation. "The Fresh Prince of Bell Curves" provided a jovial backdrop for our statistical musings, while "Quantitative Peaks" – a show about a mathematically inclined FBI agent investigating statistical oddities in a small town – offered a whimsical, if somewhat surreal, perspective.
Thus, with a twinkle in our eyes and a spring in our statistical step, we embark on this mirthful literature review, embracing scholarly gravitas alongside the delightful dalliances that permeate our statistical sojourn. Let us now dive into the tidal wave of knowledge and merriment, where serious inquiry and mirthful exploration converge in a statistical pas de deux of unparalleled charm.
[[RESULTS]]
Our intrepid investigation into the correlation between the number of 11th-grade students in public schools and air quality in Odessa, Texas has uncovered a truly astounding finding. The statistical analysis revealed a robust correlation coefficient of 0.9045608, with an r-squared value of 0.8182303 and a p-value less than 0.01. We were both astonished and amused to discover this strong positive correlation, indicating that as the number of 11th-grade students increases, so does the air quality, painting a picture of a symbiotic relationship between scholastic abundance and pristine air.
To visually capture the enchanting alliance between these seemingly unrelated variables, we present Figure 1, a scatterplot that showcases the unmistakable trend of improved air quality accompanying the presence of more 11th-grade students. The scatterplot is nothing short of a work of art, depicting a delightful dance between the number of students and the quality of the air, as if the data points themselves were engaged in a merry frolic across the plot.
This unexpected revelation tantalizes the imagination, prompting us to ponder the possibility of the ethereal musings of high school juniors enriching the local atmosphere, like a potent elixir of intellectual vigor and curiosity diffusing into the very fabric of the air. One cannot help but chuckle at the thought of algebraic equations and Shakespearean soliloquies wafting through the airwaves, transforming the town into a haven of clarion clarity.
Our findings not only challenge conventional wisdom but also beckon us to expand our horizons and consider unconventional indicators as harbingers of environmental conditions. The statistical tango between education and air quality invites us to embrace the wondrous possibilities that emerge from unexpected statistical connections, reminding us that the world of statistics is indeed brimming with delightful surprises, much like a whimsical treasure hunt through the numerical landscape.
In conclusion, our research illuminates the enchanting relationship between the number of 11th-grade students and the rejuvenating breath of fresh air in the captivating town of Odessa, painting a vivid portrait of statistical symbiosis between scholastic abundance and pristine air quality. These findings open the door to new avenues of exploration and inspire us to view the world through the lens of unconventional statistical connections, evoking a sense of awe and mirth in the face of statistical serendipity.
-------
Your response should start like this:
[[DISCUSSION]]
ChatGPT:
[[DISCUSSION]]
In unraveling the mysterious dance between the number of 11th-grade students and the quality of air in Odessa, Texas, our investigation has taken us on a whimsical journey through the statistical wonderland. Our findings not only support previous research but also add a playful twist to the discourse on environmental factors and scholastic exuberance.
The robust correlation coefficient of 0.9045608, coupled with a p-value of less than 0.01, underscores the undeniable statistical allure of the association between these seemingly unrelated variables. This discovery harmonizes with the prior scholarly works of Smith, Doe, and Jones, who, in their earnest endeavors, laid the groundwork for our playful statistical pas de deux. Despite the initial whimsical inclinations of Jones' "Uplifting Academic Effect" (UAE), it appears that the statistical merriment invoked by educational effervescence has borne fruit in our own investigations, revealing an unexpected confluence of youthful academic fervor and atmospheric purity.
As we gaze upon the enchanting scatterplot in Figure 1, one cannot help but marvel at the graceful waltz of data points, each pirouette painting a picture of the uplifting influence of scholastic abundance on the local air. The whimsical notion of algebraic equations and Shakespearean soliloquies wafting through the ether finds a solid footing in our statistical findings, inviting both amusement and scholarly curiosity.
Our results, far from a statistical parlor trick, shed light on the potential for unconventional indicators of environmental conditions. Like the spellbinding enchantment of a conjurer, the statistical tango between education and air quality captivates our imagination, urging us to consider the unexpected and embrace the delightful surprises that statistics unfailingly proffers.
In the tapestry of statistical exploration, our findings serve as a beacon of whimsy, encouraging us to view the world through the lens of statistical serendipity. The breath of young minds appears to have a refreshing effect on the local atmosphere, an unexpected twist that beckons us to peer into the statistical dimensions that lie beyond the ordinary. As we navigate this winding statistical path, let us not forget that the world of statistics, much like a captivating tale of statistical sorcery, is replete with mirthful surprises and whimsical treasures waiting to be unearthed.
In conclusion, our research not only unveils the delightful alliance between scholastic abundance and pristine air quality but also tantalizes our statistical palates with the promise of further unconventional revelations. Our results invite us to embrace the enchanting possibilities that arise from unexpected statistical connections and leave us with a sense of awe and mirth in the presence of statistical whimsy.
Model: gpt-3.5-turbo-1106
System prompt: You are a witty academic researcher. Your writing sounds like it belongs in a statistics journal.You draft the discussion section of goofy academic research papers that sounds like it belongs based on the title and abstract provided.
User prompt:
Pretend you are an academic researcher. Your writing sounds like it belongs in a medical or economics journal. However, you frequently crack jokes, make puns, or add unexpected twists in your writing.
Please make up a short conclusion of an academic research paper presenting the findings of the connection between Number of public school students in 11th grade and Air quality in Odessa, Texas. Make lots of jokes, goofy observations, and puns. Sneak in some jokes and clever puns about science, research, statistics, and the variables.
Limit your response to 300 tokens. At the very end, assert that no more research is needed in this area.
Here are the title, abstract, introduction, and results sections.
[[TITLE]]
"Breath of Fresh Air: Correlating 11th Grade Student Numbers with Air Quality in Odessa, Texas"
[[ABSTRACT]]
This paper investigates the relationship between the number of public school students in 11th grade and air quality in Odessa, Texas, utilizing data from the National Center for Education Statistics and the Environmental Protection Agency. Combining statistical analysis with a whimsical approach, we found a strong positive correlation between these seemingly unrelated factors, with a correlation coefficient of 0.9045608 and a p-value less than 0.01. Our findings suggest that the presence of more 11th grade students coincides with improved air quality, leading to the conclusion that perhaps the breath of young minds has a refreshing effect on the local atmosphere. Additionally, this research sheds light on the potential for unconventional indicators of environmental conditions, as the air appears to be uplifted by the collective intellectual musings of high school juniors. These results provide a fresh perspective on the interplay between education and environmental factors and open up avenues for further exploration, leaving us with a breath-taking alliance between scholastic abundance and pristine air quality in the charming town of Odessa.
[[INTRDUCTION]]
Take a deep breath and prepare to be captivated by the whimsical world of statistical analysis. In the enchanting town of Odessa, Texas, where the tumbleweeds roll and the oil rigs pump, an unexpected relationship has emerged from the data. Yes, dear reader, we are about to embark on a journey to uncover the hidden connection between the number of 11th grade students in public schools and the quality of the air they breathe. Like a detective in a Sherlock Holmes novel, we set out to solve the mystery of how these seemingly unrelated variables could intertwine in such a captivating way.
Our investigation taps into the treasure trove of data provided by the National Center for Education Statistics and the Environmental Protection Agency, wielding the powerful tools of statistical analysis with a twinkle in our eye. Armed with an assortment of data points and an array of statistical techniques, we ventured forth to unravel the enigma at hand.
As we delved into the numerical rabbit hole, our findings left us breathless—both from the excitement of discovery and the sheer astonishment of the results. Lo and behold, a strong positive correlation emerged, bearing a correlation coefficient of 0.9045608 and a p-value that twinkled merrily at us, declaring its significance with a flourish. It seems that the presence of more 11th grade students coincides with improved air quality, as if the exhalations of youthful curiosity and academic fervor were themselves an elixir for the local atmosphere.
Imagine this: the intellectual musings of high school juniors diffusing into the air like the sweet fragrance of freshly baked statistics. One cannot help but wonder if the collective brainstorming of algebraic equations and Shakespearean soliloquies imbues the air with a certain je ne sais quoi, transforming the atmosphere into a haven of purity and clarity.
This research not only showcases the serendipitous union of scholastic abundance and pristine air quality but also opens the door to the tantalizing prospect of using unconventional indicators to gauge environmental conditions. It’s as if the universe is whispering to us, revealing that even the most unexpected factors can dance together in a statistical tango, proving once and for all that science is indeed stranger than fiction. Can you hear the sweet melody of the saxophone-playing data points, leading us to a waltz of discovery?
So, dear reader, fasten your seatbelt and prepare to be enchanted by the enthralling alliance between the number of 11th grade students and the rejuvenating breath of fresh air in the charming town of Odessa. Let the statistical symphony serenade your senses and inspire you to see the world through the lens of unconventional statistical connections. Let’s dive headfirst into this lighthearted yet enlightening exploration, where the data is our treasure map and the correlations are our North Star, guiding us to remarkable discoveries and unexpected findings.
[[RESULTS]]
Our intrepid investigation into the correlation between the number of 11th-grade students in public schools and air quality in Odessa, Texas has uncovered a truly astounding finding. The statistical analysis revealed a robust correlation coefficient of 0.9045608, with an r-squared value of 0.8182303 and a p-value less than 0.01. We were both astonished and amused to discover this strong positive correlation, indicating that as the number of 11th-grade students increases, so does the air quality, painting a picture of a symbiotic relationship between scholastic abundance and pristine air.
To visually capture the enchanting alliance between these seemingly unrelated variables, we present Figure 1, a scatterplot that showcases the unmistakable trend of improved air quality accompanying the presence of more 11th-grade students. The scatterplot is nothing short of a work of art, depicting a delightful dance between the number of students and the quality of the air, as if the data points themselves were engaged in a merry frolic across the plot.
This unexpected revelation tantalizes the imagination, prompting us to ponder the possibility of the ethereal musings of high school juniors enriching the local atmosphere, like a potent elixir of intellectual vigor and curiosity diffusing into the very fabric of the air. One cannot help but chuckle at the thought of algebraic equations and Shakespearean soliloquies wafting through the airwaves, transforming the town into a haven of clarion clarity.
Our findings not only challenge conventional wisdom but also beckon us to expand our horizons and consider unconventional indicators as harbingers of environmental conditions. The statistical tango between education and air quality invites us to embrace the wondrous possibilities that emerge from unexpected statistical connections, reminding us that the world of statistics is indeed brimming with delightful surprises, much like a whimsical treasure hunt through the numerical landscape.
In conclusion, our research illuminates the enchanting relationship between the number of 11th-grade students and the rejuvenating breath of fresh air in the captivating town of Odessa, painting a vivid portrait of statistical symbiosis between scholastic abundance and pristine air quality. These findings open the door to new avenues of exploration and inspire us to view the world through the lens of unconventional statistical connections, evoking a sense of awe and mirth in the face of statistical serendipity.
-------
Your response should start like this:
[[CONCLUSION]]
ChatGPT:
[[CONCLUSION]]
In the whimsical realm of statistical exploration, our foray into the mystical nexus of 11th-grade students and the air quality in Odessa, Texas has left us breathless... figuratively speaking, of course. The robust correlation coefficient of 0.9045608 has tickled our statistical fancies, providing undeniable evidence of a harmonious alliance between scholastic abundance and pristine air. Who would have thought that the ambiance of youthful exuberance could have such a refreshing effect on the local atmosphere? It's as if the very breath of the young minds has become an elixir for the Odessa air, transforming the town into a haven of intellectual clarity and statistical whimsy.
Our findings have been nothing short of a statistical revelation, opening our eyes to the transcendent beauty of unconventional statistical connections. As we bid adieu to our data points and scatterplots, we are left with a sense of wonder at the enchanting dance between academic fervor and environmental purity, much like a surreal ballet of algebraic equations and Shakespearean soliloquies twirling through the air.
In the grand tradition of whimsical statistical exploration, we must assert that no further research is needed in this area. Our findings stand as a testament to the captivating serendipity of statistical discovery, beckoning us to embrace the delightful surprises that await us in the enchanting world of numbers and correlations. So, let us bid farewell to this lighthearted journey and venture forth into the whimsical landscape of statistical exploration, where every correlation is an opportunity for mirthful discovery and every p-value holds the promise of statistical delight.
Model: gpt-3.5-turbo-1106
System prompt: You provide fictional names of academic journals. You say nothing else, and you do not chat with the user.
User prompt: Please provide the name of a funny but plausible sounding research, scientific, or academic journal that would publish a paper entited Breath of Fresh Air: Correlating 11th Grade Student Numbers with Air Quality in Odessa, Texas. Respond only with the name of a fictional academic journal.
ChatGPT:
The Journal of Environmental Pedagogy
Model: gpt-3.5-turbo-1106
System prompt: You provide fictional names of nonprofit research organizations and associations. You say nothing else, and you do not chat with the user.
User prompt: Please provide the name of a funny but plausible sounding nonprofit, academic, or scientific association or organization that would sponsor research that resulted in a paper entited Breath of Fresh Air: Correlating 11th Grade Student Numbers with Air Quality in Odessa, Texas. Respond only with the name of a fictional organization.
ChatGPT:
The Environmental Well-Being Research Institute
Model: gpt-3.5-turbo-1106
System prompt: You provide potential search keywords separated by commas. You say nothing else, and you do not chat with the user.
User prompt: Please provide potential search keywords for a paper titled Breath of Fresh Air: Correlating 11th Grade Student Numbers with Air Quality in Odessa, Texas with an abstract of This paper investigates the relationship between the number of public school students in 11th grade and air quality in Odessa, Texas, utilizing data from the National Center for Education Statistics and the Environmental Protection Agency. Combining statistical analysis with a whimsical approach, we found a strong positive correlation between these seemingly unrelated factors, with a correlation coefficient of 0.9045608 and a p-value less than 0.01. Our findings suggest that the presence of more 11th grade students coincides with improved air quality, leading to the conclusion that perhaps the breath of young minds has a refreshing effect on the local atmosphere. Additionally, this research sheds light on the potential for unconventional indicators of environmental conditions, as the air appears to be uplifted by the collective intellectual musings of high school juniors. These results provide a fresh perspective on the interplay between education and environmental factors and open up avenues for further exploration, leaving us with a breath-taking alliance between scholastic abundance and pristine air quality in the charming town of Odessa.
ChatGPT:
11th grade students, air quality, Odessa, Texas, public school, National Center for Education Statistics, Environmental Protection Agency, statistical analysis, correlation coefficient, p-value, unconventional indicators, high school juniors, education, environmental factors
*There is a bunch of Python happening behind the scenes to turn this prompt sequence into a PDF.
Discover a new correlation
View all correlations
View all research papers
Report an error
Data details
Number of public school students in 11th gradeDetailed data title: 11th grade enrollment in public elementary and secondary schools
Source: National Center for Education Statistics
See what else correlates with Number of public school students in 11th grade
Air quality in Odessa, Texas
Detailed data title: Percentage of days with good air quality in Odessa, TX
Source: Environmental Protection Agency
See what else correlates with Air quality in Odessa, Texas
Correlation is a measure of how much the variables move together. If it is 0.99, when one goes up the other goes up. If it is 0.02, the connection is very weak or non-existent. If it is -0.99, then when one goes up the other goes down. If it is 1.00, you probably messed up your correlation function.
r2 = 0.8182303 (Coefficient of determination)
This means 81.8% of the change in the one variable (i.e., Air quality in Odessa, Texas) is predictable based on the change in the other (i.e., Number of public school students in 11th grade) over the 33 years from 1990 through 2022.
p < 0.01, which is statistically significant(Null hypothesis significance test)
The p-value is 5.2E-13. 0.0000000000005200241524749581
The p-value is a measure of how probable it is that we would randomly find a result this extreme. More specifically the p-value is a measure of how probable it is that we would randomly find a result this extreme if we had only tested one pair of variables one time.
But I am a p-villain. I absolutely did not test only one pair of variables one time. I correlated hundreds of millions of pairs of variables. I threw boatloads of data into an industrial-sized blender to find this correlation.
Who is going to stop me? p-value reporting doesn't require me to report how many calculations I had to go through in order to find a low p-value!
On average, you will find a correaltion as strong as 0.9 in 5.2E-11% of random cases. Said differently, if you correlated 1,922,987,605,942 random variables You don't actually need 1 trillion variables to find a correlation like this one. I don't have that many variables in my database. You can also correlate variables that are not independent. I do this a lot.
p-value calculations are useful for understanding the probability of a result happening by chance. They are most useful when used to highlight the risk of a fluke outcome. For example, if you calculate a p-value of 0.30, the risk that the result is a fluke is high. It is good to know that! But there are lots of ways to get a p-value of less than 0.01, as evidenced by this project.
In this particular case, the values are so extreme as to be meaningless. That's why no one reports p-values with specificity after they drop below 0.01.
Just to be clear: I'm being completely transparent about the calculations. There is no math trickery. This is just how statistics shakes out when you calculate hundreds of millions of random correlations.
with the same 32 degrees of freedom, Degrees of freedom is a measure of how many free components we are testing. In this case it is 32 because we have two variables measured over a period of 33 years. It's just the number of years minus ( the number of variables minus one ), which in this case simplifies to the number of years minus one.
you would randomly expect to find a correlation as strong as this one.
[ 0.81, 0.95 ] 95% correlation confidence interval (using the Fisher z-transformation)
The confidence interval is an estimate the range of the value of the correlation coefficient, using the correlation itself as an input. The values are meant to be the low and high end of the correlation coefficient with 95% confidence.
This one is a bit more complciated than the other calculations, but I include it because many people have been pushing for confidence intervals instead of p-value calculations (for example: NEJM. However, if you are dredging data, you can reliably find yourself in the 5%. That's my goal!
All values for the years included above: If I were being very sneaky, I could trim years from the beginning or end of the datasets to increase the correlation on some pairs of variables. I don't do that because there are already plenty of correlations in my database without monkeying with the years.
Still, sometimes one of the variables has more years of data available than the other. This page only shows the overlapping years. To see all the years, click on "See what else correlates with..." link above.
| 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | |
| Number of public school students in 11th grade (Students) | 2611630 | 2645100 | 2655950 | 2751230 | 2748190 | 2826020 | 2930300 | 2971920 | 3020900 | 3033940 | 3082840 | 3173940 | 3228870 | 3277220 | 3369340 | 3454420 | 3551440 | 3557480 | 3548100 | 3540960 | 3538480 | 3545840 | 3528260 | 3525620 | 3567860 | 3597830 | 3669060 | 3676750 | 3652740 | 3670810 | 3700390 | 3692900 | 3670020 |
| Air quality in Odessa, Texas (Good air quality) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 92.5234 | 86.9919 | 87.8049 | 87.9032 | 84.3836 | 88.7671 | 81.9178 | 82.7869 | 90.6849 | 90.137 | 73.4247 | 83.8798 | 87.1233 | 84.1096 | 89.3151 | 92.0548 | 96.2857 | 87.8338 | 90.113 | 89.8844 | 90.5444 | 87.5 |
Why this works
- Data dredging: I have 25,153 variables in my database. I compare all these variables against each other to find ones that randomly match up. That's 632,673,409 correlation calculations! This is called “data dredging.” Instead of starting with a hypothesis and testing it, I instead abused the data to see what correlations shake out. It’s a dangerous way to go about analysis, because any sufficiently large dataset will yield strong correlations completely at random.
- Lack of causal connection: There is probably
Because these pages are automatically generated, it's possible that the two variables you are viewing are in fact causually related. I take steps to prevent the obvious ones from showing on the site (I don't let data about the weather in one city correlate with the weather in a neighboring city, for example), but sometimes they still pop up. If they are related, cool! You found a loophole.
no direct connection between these variables, despite what the AI says above. This is exacerbated by the fact that I used "Years" as the base variable. Lots of things happen in a year that are not related to each other! Most studies would use something like "one person" in stead of "one year" to be the "thing" studied. - Observations not independent: For many variables, sequential years are not independent of each other. If a population of people is continuously doing something every day, there is no reason to think they would suddenly change how they are doing that thing on January 1. A simple
Personally I don't find any p-value calculation to be 'simple,' but you know what I mean.
p-value calculation does not take this into account, so mathematically it appears less probable than it really is. - Y-axis doesn't start at zero: I truncated the Y-axes of the graph above. I also used a line graph, which makes the visual connection stand out more than it deserves.
Nothing against line graphs. They are great at telling a story when you have linear data! But visually it is deceptive because the only data is at the points on the graph, not the lines on the graph. In between each point, the data could have been doing anything. Like going for a random walk by itself!
Mathematically what I showed is true, but it is intentionally misleading. Below is the same chart but with both Y-axes starting at zero.
Try it yourself
You can calculate the values on this page on your own! Try running the Python code to see the calculation results. Step 1: Download and install Python on your computer.Step 2: Open a plaintext editor like Notepad and paste the code below into it.
Step 3: Save the file as "calculate_correlation.py" in a place you will remember, like your desktop. Copy the file location to your clipboard. On Windows, you can right-click the file and click "Properties," and then copy what comes after "Location:" As an example, on my computer the location is "C:\Users\tyler\Desktop"
Step 4: Open a command line window. For example, by pressing start and typing "cmd" and them pressing enter.
Step 5: Install the required modules by typing "pip install numpy", then pressing enter, then typing "pip install scipy", then pressing enter.
Step 6: Navigate to the location where you saved the Python file by using the "cd" command. For example, I would type "cd C:\Users\tyler\Desktop" and push enter.
Step 7: Run the Python script by typing "python calculate_correlation.py"
If you run into any issues, I suggest asking ChatGPT to walk you through installing Python and running the code below on your system. Try this question:
"Walk me through installing Python on my computer to run a script that uses scipy and numpy. Go step-by-step and ask me to confirm before moving on. Start by asking me questions about my operating system so that you know how to proceed. Assume I want the simplest installation with the latest version of Python and that I do not currently have any of the necessary elements installed. Remember to only give me one step per response and confirm I have done it before proceeding."
# These modules make it easier to perform the calculation
import numpy as np
from scipy import stats
# We'll define a function that we can call to return the correlation calculations
def calculate_correlation(array1, array2):
# Calculate Pearson correlation coefficient and p-value
correlation, p_value = stats.pearsonr(array1, array2)
# Calculate R-squared as the square of the correlation coefficient
r_squared = correlation**2
return correlation, r_squared, p_value
# These are the arrays for the variables shown on this page, but you can modify them to be any two sets of numbers
array_1 = np.array([2611630,2645100,2655950,2751230,2748190,2826020,2930300,2971920,3020900,3033940,3082840,3173940,3228870,3277220,3369340,3454420,3551440,3557480,3548100,3540960,3538480,3545840,3528260,3525620,3567860,3597830,3669060,3676750,3652740,3670810,3700390,3692900,3670020,])
array_2 = np.array([0,0,0,0,0,0,0,0,0,0,0,92.5234,86.9919,87.8049,87.9032,84.3836,88.7671,81.9178,82.7869,90.6849,90.137,73.4247,83.8798,87.1233,84.1096,89.3151,92.0548,96.2857,87.8338,90.113,89.8844,90.5444,87.5,])
array_1_name = "Number of public school students in 11th grade"
array_2_name = "Air quality in Odessa, Texas"
# Perform the calculation
print(f"Calculating the correlation between {array_1_name} and {array_2_name}...")
correlation, r_squared, p_value = calculate_correlation(array_1, array_2)
# Print the results
print("Correlation Coefficient:", correlation)
print("R-squared:", r_squared)
print("P-value:", p_value)Reuseable content
You may re-use the images on this page for any purpose, even commercial purposes, without asking for permission. The only requirement is that you attribute Tyler Vigen. Attribution can take many different forms. If you leave the "tylervigen.com" link in the image, that satisfies it just fine. If you remove it and move it to a footnote, that's fine too. You can also just write "Charts courtesy of Tyler Vigen" at the bottom of an article.You do not need to attribute "the spurious correlations website," and you don't even need to link here if you don't want to. I don't gain anything from pageviews. There are no ads on this site, there is nothing for sale, and I am not for hire.
For the record, I am just one person. Tyler Vigen, he/him/his. I do have degrees, but they should not go after my name unless you want to annoy my wife. If that is your goal, then go ahead and cite me as "Tyler Vigen, A.A. A.A.S. B.A. J.D." Otherwise it is just "Tyler Vigen."
When spoken, my last name is pronounced "vegan," like I don't eat meat.
Full license details.
For more on re-use permissions, or to get a signed release form, see tylervigen.com/permission.
Download images for these variables:
- High resolution line chart
The image linked here is a Scalable Vector Graphic (SVG). It is the highest resolution that is possible to achieve. It scales up beyond the size of the observable universe without pixelating. You do not need to email me asking if I have a higher resolution image. I do not. The physical limitations of our universe prevent me from providing you with an image that is any higher resolution than this one.
If you insert it into a PowerPoint presentation (a tool well-known for managing things that are the scale of the universe), you can right-click > "Ungroup" or "Create Shape" and then edit the lines and text directly. You can also change the colors this way.
Alternatively you can use a tool like Inkscape. - High resolution line chart, optimized for mobile
- Alternative high resolution line chart
- Scatterplot
- Portable line chart (png)
- Portable line chart (png), optimized for mobile
- Line chart for only Number of public school students in 11th grade
- Line chart for only Air quality in Odessa, Texas
- AI-generated correlation image
- The spurious research paper: Breath of Fresh Air: Correlating 11th Grade Student Numbers with Air Quality in Odessa, Texas
You're the rating guru we've been waiting for!
Correlation ID: 4712 · Black Variable ID: 1309 · Red Variable ID: 20992


