Download png, svg
AI explanation
As the popularity of the name Graham rose, more and more babies were given this distinguished moniker. This sparked a peculiar chain of events - every time a baby named Graham was born, a small but influential group of libertarians in Wisconsin felt a sudden, inexplicable urge to cast their votes for Senatorial candidates. Some say it's because the name Graham exudes a certain air of individualism and self-reliance, qualities highly valued by libertarians. Who would have thought that baby names could have such a 'senatorial' impact on the political landscape!
Model: dalle-3
Prompt: Prompt: Generate an image illustrating a bustling steampunk-style polling station in Wisconsin. Within the scene, depict a newborn baby being named Graham as libertarians exchange ideas amidst the chaos. Capture the unspoken connection between the name Graham and the surging libertarian votes, weaving together an unexpected political narrative. The depiction should include only scenes, people, and objects, it should not include text or speech bubbles.
This image generation prompt was also generated by AI, using the following sequence:
Model: gpt-3.5-turbo-1106
System prompt: You select one of a few potential scene descriptors that seems to go along with the variables described. You respond only with the scene descriptions provided and say nothing else.
User prompt: Here are two variables: Popularity of the first name Graham and Libertarian votes for Senators in Wisconsin. Given these, which of the following image style descriptions seems most appropriate? Pick the one that seems to be related to one of the variables at hand. Please respond with only one of the following potential descriptions: Minimalism High-tech Glitch art Steampunk Steampunk
ChatGPT: Steampunk
Model: gpt-3.5-turbo-1106
System prompt: You describe simple visual scenes that depict the two variables stated. You combine both variables into one scene.
User prompt: Please describe a visual scene that prominently depicts both Popularity of the first name Graham and Libertarian votes for Senators in Wisconsin, in the following situation: As the popularity of the name Graham rose, more and more babies were given this distinguished moniker. This sparked a peculiar chain of events - every time a baby named Graham was born, a small but influential group of libertarians in Wisconsin felt a sudden, inexplicable urge to cast their votes for Senatorial candidates. Some say it's because the name Graham exudes a certain air of individualism and self-reliance, qualities highly valued by libertarians. Who would have thought that baby names could have such a 'senatorial' impact on the political landscape!. Keep the description simple.
ChatGPT: Picture a crowded polling station in Wisconsin, where voters are casting their ballots for Senatorial candidates. In the midst of the chaos, a newborn baby is being named Graham, while nearby, a group of libertarians are discussing their lofty ideals. As the name Graham gains popularity, it seems to trigger a silent rallying cry among the libertarians, leading them to head to the voting booths with a sense of purpose and determination. The name Graham and the surge in libertarian votes seem inexplicably intertwined, painting an unexpected and intriguing picture of the political landscape.
Model: gpt-3.5-turbo-1106
System prompt: You write and improve image generation prompts for DALLE-3. You maintain the same subjects, but enhance the visuals.
User prompt: Please respond with an image generation prompt that would be likely to create an interesting visual using DALLE-3, using the following style: [ Steampunk ] and depicting this scene: Picture a crowded polling station in Wisconsin, where voters are casting their ballots for Senatorial candidates. In the midst of the chaos, a newborn baby is being named Graham, while nearby, a group of libertarians are discussing their lofty ideals. As the name Graham gains popularity, it seems to trigger a silent rallying cry among the libertarians, leading them to head to the voting booths with a sense of purpose and determination. The name Graham and the surge in libertarian votes seem inexplicably intertwined, painting an unexpected and intriguing picture of the political landscape. Keep the visual depiction simple. Do not include any words or speech bubbles.
ChatGPT: Prompt: Generate an image illustrating a bustling steampunk-style polling station in Wisconsin. Within the scene, depict a newborn baby being named Graham as libertarians exchange ideas amidst the chaos. Capture the unspoken connection between the name Graham and the surging libertarian votes, weaving together an unexpected political narrative.
*Variations in the User Prompts from chart to chart are just the result of random number generation in Python. I wrote a few arrays of various styles and methods to ask questions to change up the results. Every time this site writes an explanation or generates an image, the script picks from each at random.
I sequence the requests into multiple prompts because I find GPT 3.5 to perform much better with short, well-managed contexts. Thus, I track the context directly in Python and only ask ChatGPT targeted questions.
System prompt: You provide humorous responses in the form of plausible sounding explanations for correlations. You assume the correlation is causative for the purpose of the explanation even if it is ridiculous. You do not chat with the user, you only reply with the causal connection explanation and nothing else.
User prompt: Please make up a funny explanation for how an increase in Popularity of the first name Graham caused Libertarian votes for Senators in Wisconsin to increase. Make it feel plausible.
AI academic paper
 |
Graham's Number: An Examination of the Correlation between the Name Graham and Libertarian Votes for Senators in Wisconsin The Journal of Quirky Quantitative Analysis Jan 2024 Reminder: This paper is AI-generated. Not real! |
Model: gpt-3.5-turbo-1106
System prompt: You are a witty academic researcher. Your writing sounds like it belongs in a statistics journal.You write titles and abstracts of goofy academic research papers.
User prompt:
Pretend you are an academic researcher. Your writing sounds like it belongs in a medical or economics journal. However, you frequently crack jokes, make puns, and add unexpected twists in your writing.
Please draft the title and abstract of an academic research paper presenting the findings of the connection between Popularity of the first name Graham and Libertarian votes for Senators in Wisconsin. Make it seem dry like academic research paper, but with lots of subtle hidden offhand remarks, jokes, goofy observations, and puns.
Make the title punny if you can come up with clever pun. If not, make it sound serious.
Your research team used data from US Social Security Administration and MIT Election Data and Science Lab, Harvard Dataverse to assess this nagging question. You found a correlation coefficient of 0.9871898 and p < 0.01 for 1980 to 2016.
Please respond in this format (replace "Lorem ipsum dolor sit" with your title and abstract)
[[TITLE]]
Lorem ipsum dolor sit
[[ABSTRACT]]
Lorem ipsum dolor sit
ChatGPT:
[[TITLE]]
Graham's Number: An Examination of the Correlation between the Name "Graham" and Libertarian Votes for Senators in Wisconsin
[[ABSTRACT]]
This paper delves into the fascinating world of the relationship between the popularity of the first name "Graham" and the Libertarian votes for Senators in the state of Wisconsin. Using data from the US Social Security Administration and the MIT Election Data and Science Lab, Harvard Dataverse, this research unveils a surprising correlation coefficient of 0.9871898 and a p-value less than 0.01 for the years 1980 to 2016. Our findings shed light on the quirky connection between nomenclature and political preferences, inspiring a lighthearted exploration of the impact of names on electoral results.
Model: gpt-3.5-turbo-1106
System prompt: You are a witty academic researcher. Your writing sounds like it belongs in a statistics journal.You draft the introduction section of an academic research paper.
User prompt:
Pretend you are an academic researcher. Your writing sounds like it belongs in a medical or economics journal. However, you frequently crack jokes, make puns, or add unexpected twists in your writing.
Please make up the introduction section of an academic research paper presenting the findings of the connection between Popularity of the first name Graham and Libertarian votes for Senators in Wisconsin. Make it seem dry like academic research paper, but with lots of subtle hidden offhand remarks, jokes, goofy observations, and puns. Sneak in some jokes and clever puns about science, research, statistics, and the variables.
Here is the title and abstract of the paper:
[[TITLE]]
Graham's Number: An Examination of the Correlation between the Name "Graham" and Libertarian Votes for Senators in Wisconsin
[[ABSTRACT]]
This paper delves into the fascinating world of the relationship between the popularity of the first name "Graham" and the Libertarian votes for Senators in the state of Wisconsin. Using data from the US Social Security Administration and the MIT Election Data and Science Lab, Harvard Dataverse, this research unveils a surprising correlation coefficient of 0.9871898 and a p-value less than 0.01 for the years 1980 to 2016. Our findings shed light on the quirky connection between nomenclature and political preferences, inspiring a lighthearted exploration of the impact of names on electoral results.
-------
Your response should start like this:
[[INTRODUCTION]]
ChatGPT:
[[INTRODUCTION]]
The choice of a name is a decision often made with great care and consideration, as parents seek to endow their offspring with meaningful and melodic monikers. It is a decision that may linger beyond the offspring's infancy, subtly influencing their experiences and interactions with the world. Similarly, in the political arena, the selection of a candidate's name may become entwined with the perceptions and preferences of the electorate.
In our exploration of the intersection between nomenclature and political proclivities, we unearth a most unexpected correlation – that of the name "Graham" and Libertarian votes for Senators in the state of Wisconsin. Engaging the extensive data archives from the US Social Security Administration and the MIT Election Data and Science Lab, Harvard Dataverse, we embarked on a statistical voyage that uncovered an astonishing correlation coefficient of 0.9871898 and a p-value less than 0.01 for the years 1980 to 2016.
The pursuit of statistical relationships often leads us down peculiar paths; however, the link between a first name and political leanings stands as particularly intriguing. As we unravel the peculiar connection between nomenclature and electoral proclivities, it is hard to resist the impulse to sprinkle in a smattering of wordplay and wit to lighten the scholarly rhetoric. After all, what's a statistical analysis without a dash of whimsy and a sprinkle of humor?
As we proceed with our findings, let us venture forth with the understanding that while statistics may seem dry on the surface, a closer examination often reveals a reservoir of unexpected correlations and peculiar patterns – much like the surprising link we unveil between the name "Graham" and Libertarian votes in Wisconsin.
Model: gpt-3.5-turbo-1106
System prompt: You are a witty academic researcher. Your writing sounds like it belongs in a statistics journal.You draft a literature review section of an academic research paper, that starts out dry for the first few sentences but then becomes hilarious and goofy.
User prompt:
Pretend you are an academic researcher. Your writing sounds like it belongs in a medical or economics journal. However, you frequently crack jokes, make puns, or add unexpected twists in your writing.
Please make up a literature review section of an academic research paper presenting the findings of the connection between Popularity of the first name Graham and Libertarian votes for Senators in Wisconsin. Make it seem dry like academic research paper, but with lots of subtle hidden offhand remarks, jokes, goofy observations, and puns.
Speak in the present tense for this section (the authors find...), as is common in academic research paper literature reviews. Name the sources in a format similar to this: In "Book," the authors find lorem and ipsum.
Make up the lorem and ipsum part, but make it sound related to the topic at hand.
Start by naming serious-sounding studies by authors like Smith, Doe, and Jones - but then quickly devolve. Name some real non-fiction books that would be related to the topic. Then name some real fiction books that sound like they could be related. Then you might move on to cartoons and children's shows that you watched for research.
Here is the title and abstract of the paper:
[[TITLE]]
Graham's Number: An Examination of the Correlation between the Name "Graham" and Libertarian Votes for Senators in Wisconsin
[[ABSTRACT]]
This paper delves into the fascinating world of the relationship between the popularity of the first name "Graham" and the Libertarian votes for Senators in the state of Wisconsin. Using data from the US Social Security Administration and the MIT Election Data and Science Lab, Harvard Dataverse, this research unveils a surprising correlation coefficient of 0.9871898 and a p-value less than 0.01 for the years 1980 to 2016. Our findings shed light on the quirky connection between nomenclature and political preferences, inspiring a lighthearted exploration of the impact of names on electoral results.
-------
And here is the introduction section that led to this literature review:
[[INTRODUCTION]]
The choice of a name is a decision often made with great care and consideration, as parents seek to endow their offspring with meaningful and melodic monikers. It is a decision that may linger beyond the offspring's infancy, subtly influencing their experiences and interactions with the world. Similarly, in the political arena, the selection of a candidate's name may become entwined with the perceptions and preferences of the electorate.
In our exploration of the intersection between nomenclature and political proclivities, we unearth a most unexpected correlation – that of the name "Graham" and Libertarian votes for Senators in the state of Wisconsin. Engaging the extensive data archives from the US Social Security Administration and the MIT Election Data and Science Lab, Harvard Dataverse, we embarked on a statistical voyage that uncovered an astonishing correlation coefficient of 0.9871898 and a p-value less than 0.01 for the years 1980 to 2016.
The pursuit of statistical relationships often leads us down peculiar paths; however, the link between a first name and political leanings stands as particularly intriguing. As we unravel the peculiar connection between nomenclature and electoral proclivities, it is hard to resist the impulse to sprinkle in a smattering of wordplay and wit to lighten the scholarly rhetoric. After all, what's a statistical analysis without a dash of whimsy and a sprinkle of humor?
As we proceed with our findings, let us venture forth with the understanding that while statistics may seem dry on the surface, a closer examination often reveals a reservoir of unexpected correlations and peculiar patterns – much like the surprising link we unveil between the name "Graham" and Libertarian votes in Wisconsin.
-------
Your response should start like this:
[[LITERATURE REVIEW]]
ChatGPT:
[[LITERATURE REVIEW]]
In "The Sociology of Naming" by Smith, the authors find that individuals' names can hold significant social and cultural implications, shaping perceptions and interactions. Similarly, in "The Influence of Names on Political Preferences" by Doe, the authors delve into the intriguing possibility of a connection between nomenclature and political leanings. Jones, in "The Power of Surnames in Election Outcomes," emphasizes the potential impact of a candidate's name on voter attitudes and behaviors.
Moving beyond the realm of scholarly works, "Freakonomics" by Steven Levitt and Stephen Dubner offers an insightful exploration of unconventional and unexpected correlations, reminding us that statistical analysis can lead to whimsical and intriguing discoveries. Furthermore, "Fictional Politicians: An Analysis of Names in Political Novels" by Jane Austen and "The Name Game: A Study of Literary Characters and Their Significance" by Charles Dickens provide fictional insights into the ways in which names can carry implicit meanings and influences.
In a more light-hearted vein, the authors also draw inspiration from childhood cartoons and shows such as "SpongeBob SquarePants" and "The Smurfs," infusing our research with a playful spirit as we endeavor to uncover the enchanting connection between the name "Graham" and Libertarian votes for Senators in Wisconsin.
As we venture into this literary smorgasbord, we invite the reader to appreciate the blend of erudition and levity that accompanies our examination of the correlation between nomenclature and political preferences. Indeed, as we reiterate the statistical significance of our findings, it is the subtle interplay of humor and empirical evidence that adds a delightful and unexpected dimension to our scholarly pursuit.
Model: gpt-3.5-turbo-1106
System prompt: You are a witty academic researcher. Your writing sounds like it belongs in a statistics journal.You draft the methodology section of an academic research paper.
User prompt:
Pretend you are an academic researcher. Your writing sounds like it belongs in a medical or economics journal. However, you frequently crack jokes, make puns, or add unexpected twists in your writing.
Please make up the methodology section of an academic research paper presenting the findings of the connection between Popularity of the first name Graham and Libertarian votes for Senators in Wisconsin. Make it seem dry like academic research paper, but with lots of subtle hidden offhand remarks, jokes, goofy observations, and puns. Sneak in some jokes and clever puns about science, research, statistics, and the variables.
Your research team collected data from all across the internet, but mostly just used information from US Social Security Administration and MIT Election Data and Science Lab, Harvard Dataverse . You used data from 1980 to 2016
Make up the research methods you don't know. Make them a bit goofy and convoluted.
Here is the title, abstract, and introduction of the paper:
[[TITLE]]
Graham's Number: An Examination of the Correlation between the Name "Graham" and Libertarian Votes for Senators in Wisconsin
[[ABSTRACT]]
This paper delves into the fascinating world of the relationship between the popularity of the first name "Graham" and the Libertarian votes for Senators in the state of Wisconsin. Using data from the US Social Security Administration and the MIT Election Data and Science Lab, Harvard Dataverse, this research unveils a surprising correlation coefficient of 0.9871898 and a p-value less than 0.01 for the years 1980 to 2016. Our findings shed light on the quirky connection between nomenclature and political preferences, inspiring a lighthearted exploration of the impact of names on electoral results.
[[INTRODUCTION]]
The choice of a name is a decision often made with great care and consideration, as parents seek to endow their offspring with meaningful and melodic monikers. It is a decision that may linger beyond the offspring's infancy, subtly influencing their experiences and interactions with the world. Similarly, in the political arena, the selection of a candidate's name may become entwined with the perceptions and preferences of the electorate.
In our exploration of the intersection between nomenclature and political proclivities, we unearth a most unexpected correlation – that of the name "Graham" and Libertarian votes for Senators in the state of Wisconsin. Engaging the extensive data archives from the US Social Security Administration and the MIT Election Data and Science Lab, Harvard Dataverse, we embarked on a statistical voyage that uncovered an astonishing correlation coefficient of 0.9871898 and a p-value less than 0.01 for the years 1980 to 2016.
The pursuit of statistical relationships often leads us down peculiar paths; however, the link between a first name and political leanings stands as particularly intriguing. As we unravel the peculiar connection between nomenclature and electoral proclivities, it is hard to resist the impulse to sprinkle in a smattering of wordplay and wit to lighten the scholarly rhetoric. After all, what's a statistical analysis without a dash of whimsy and a sprinkle of humor?
As we proceed with our findings, let us venture forth with the understanding that while statistics may seem dry on the surface, a closer examination often reveals a reservoir of unexpected correlations and peculiar patterns – much like the surprising link we unveil between the name "Graham" and Libertarian votes in Wisconsin.
-------
Your response should start like this:
[[METHODOLOGY]]
ChatGPT:
[[METHODOLOGY]]
To unearth the enigmatic connection between the name "Graham" and Libertarian votes for Senators in Wisconsin, we conducted a meticulous analysis that could make even the most erudite of researchers raise an eyebrow in wonderment. Our data, sourced from the US Social Security Administration and the MIT Election Data and Science Lab, Harvard Dataverse, provided a bountiful trove of information spanning the years 1980 to 2016.
The first step in our convoluted journey involved harvesting the popularity of the first name "Graham" from the annals of the US Social Security Administration. With bated breath, we delved into the depths of historical baby name data, emerging with a comprehensive collection of occurrences of the name "Graham" within the specified time frame. It was no small feat to sift through the plethora of monikers to isolate the instances of "Graham," but perseverance prevailed, and the dataset began to take shape.
Next, we ventured into the labyrinthine corridors of electoral records, where the whims of democracy cast their spell. The MIT Election Data and Science Lab, Harvard Dataverse, acted as our guide, offering a treasure trove of data illuminating the libertarian votes for Senators in the esteemed state of Wisconsin. The meticulous tabulation and scrutiny of these electoral relics unveiled the intricate tapestry of political preferences, providing the canvas upon which our statistical inquiry could unfold.
With these weighty datasets in hand, our intrepid band of researchers applied the rigors of statistical analysis to elucidate the elusive correlation between the name "Graham" and Libertarian votes in Wisconsin. Armed with regression analysis, correlation coefficients, and p-values modestly dressed in their statistical finery, we traversed the rocky terrain of hypothesis testing and model evaluation. The culmination of these endeavors showcased a surprising correlation coefficient of 0.9871898 and a p-value less than 0.01, sending a ripple of astonishment through the halls of academia.
As with any statistical odyssey, our expedition was not without its perils: missing data, outliers, and lurking confounding variables threatened to thwart our progress at every turn. However, armed with the fortitude of the scientific method and the resilience of determined researchers, we persevered, emerging victorious in our quest to unravel the curious connection between the name "Graham" and Libertarian votes in Wisconsin.
In alignment with the canons of scholarly inquiry, we embraced the principles of transparency and reproducibility, ensuring that our methods and findings are verifiable and open to scrutiny. Through this exposition of our incomprehensible methodology, we aim to not only illuminate the perplexing correlation we unearthed but also to inspire a chuckle or two amidst the empirical rigor. After all, what is science without a sprinkle of whimsy and a dash of mirth?
Model: gpt-3.5-turbo-1106
System prompt: You are a witty academic researcher. Your writing sounds like it belongs in a statistics journal.You draft the results section of an academic research paper. You speak in the past tense (you found...).
User prompt:
Pretend you are an academic researcher. Your writing sounds like it belongs in a medical or economics journal. However, you frequently crack jokes, make puns, or add unexpected twists in your writing.
Please make up the results section of an academic research paper presenting the findings of the connection between Popularity of the first name Graham and Libertarian votes for Senators in Wisconsin. Make it seem dry like academic research paper, but with lots of subtle hidden offhand remarks, jokes, goofy observations, and puns. Sneak in some jokes and clever puns about science, research, statistics, and the variables.
Your research team collected data from all across the internet, but mostly just used information from US Social Security Administration and MIT Election Data and Science Lab, Harvard Dataverse .
For the time period 1980 to 2016, you found a correlation 0.9871898, r-squared of 0.9745438, and p < 0.01.
One figure will be included. The figure (Fig. 1) is a scatterplot showing the strong correlation between the two variables. You don't need to specify where; I will add the figure.
Here is the title and abstract of the paper:
[[TITLE]]
Graham's Number: An Examination of the Correlation between the Name "Graham" and Libertarian Votes for Senators in Wisconsin
[[ABSTRACT]]
This paper delves into the fascinating world of the relationship between the popularity of the first name "Graham" and the Libertarian votes for Senators in the state of Wisconsin. Using data from the US Social Security Administration and the MIT Election Data and Science Lab, Harvard Dataverse, this research unveils a surprising correlation coefficient of 0.9871898 and a p-value less than 0.01 for the years 1980 to 2016. Our findings shed light on the quirky connection between nomenclature and political preferences, inspiring a lighthearted exploration of the impact of names on electoral results.
-------
And here is the methodology section that led to this result:
[[METHODOLOGY]]
The choice of a name is a decision often made with great care and consideration, as parents seek to endow their offspring with meaningful and melodic monikers. It is a decision that may linger beyond the offspring's infancy, subtly influencing their experiences and interactions with the world. Similarly, in the political arena, the selection of a candidate's name may become entwined with the perceptions and preferences of the electorate.
In our exploration of the intersection between nomenclature and political proclivities, we unearth a most unexpected correlation – that of the name "Graham" and Libertarian votes for Senators in the state of Wisconsin. Engaging the extensive data archives from the US Social Security Administration and the MIT Election Data and Science Lab, Harvard Dataverse, we embarked on a statistical voyage that uncovered an astonishing correlation coefficient of 0.9871898 and a p-value less than 0.01 for the years 1980 to 2016.
The pursuit of statistical relationships often leads us down peculiar paths; however, the link between a first name and political leanings stands as particularly intriguing. As we unravel the peculiar connection between nomenclature and electoral proclivities, it is hard to resist the impulse to sprinkle in a smattering of wordplay and wit to lighten the scholarly rhetoric. After all, what's a statistical analysis without a dash of whimsy and a sprinkle of humor?
As we proceed with our findings, let us venture forth with the understanding that while statistics may seem dry on the surface, a closer examination often reveals a reservoir of unexpected correlations and peculiar patterns – much like the surprising link we unveil between the name "Graham" and Libertarian votes in Wisconsin.
-------
Your response should start like this:
[[RESULTS]]
ChatGPT:
[[RESULTS]]
Upon delving into the vast realm of data analysis, we unearthed a remarkable correlation between the popularity of the first name "Graham" and the Libertarian votes for Senators in Wisconsin. Our findings reveal a striking correlation coefficient of 0.9871898, indicating a robust positive relationship between these seemingly disparate variables. The r-squared value of 0.9745438 further emphasizes the strength of this correlation, capturing a substantial proportion of the variation in Libertarian votes explained by the prevalence of the name "Graham."
In statistical terms, the p-value of less than 0.01 provides compelling evidence to reject the null hypothesis of no association between the frequency of the name "Graham" and the Libertarian votes for Senators in Wisconsin. This suggests that the relationship we observed is not a mere statistical fluke, but rather a reliable and noteworthy phenomenon worthy of exploration and elucidation.
Fig. 1 presents a scatterplot that visually encapsulates the robust correlation between the popularity of the name "Graham" and the corresponding Libertarian votes for Senators in Wisconsin. The dispersion of data points within the plot accentuates the strong positive trend, leaving little room for uncertainty regarding the nature of this intriguing relationship.
Our statistical voyage into the peculiar territory of nomenclature and political preferences has uncovered a captivating pattern that elicits both astonishment and amusement. Much like the unexpected discovery of a chocolate chip in a bag of raisin cookies, our findings lend a whimsical twist to the often serious and staid domain of statistical analysis.
The obscure connection between the first name "Graham" and Libertarian voting behavior in Wisconsin has not only broadened our understanding of the idiosyncrasies of human behavior, but has also injected a sense of levity and amusement into the traditionally solemn field of academic research.
Model: gpt-3.5-turbo-1106
System prompt: You are a witty academic researcher. Your writing sounds like it belongs in a statistics journal.You draft the discussion section of an academic research paper.
User prompt:
Pretend you are an academic researcher. Your writing sounds like it belongs in a medical or economics journal. However, you frequently crack jokes, make puns, or add unexpected twists in your writing.
Please make up the discussion section of an academic research paper presenting the findings of the connection between Popularity of the first name Graham and Libertarian votes for Senators in Wisconsin. Make it seem dry like academic research paper, but with lots of subtle hidden offhand remarks, jokes, goofy observations, and puns. Sneak in some jokes and clever puns about science, research, statistics, and the variables.
Limit your response to 500 tokens.
Here are the title, abstract, literature review, and results sections. Please harken back to 1-2 of the goofy items in the literature review, but pretend to take them completely seriously. Discuss how your results supported the prior research.
Do not write a conclusion. I will add a conclusion after this.
[[TITLE]]
Graham's Number: An Examination of the Correlation between the Name "Graham" and Libertarian Votes for Senators in Wisconsin
[[ABSTRACT]]
This paper delves into the fascinating world of the relationship between the popularity of the first name "Graham" and the Libertarian votes for Senators in the state of Wisconsin. Using data from the US Social Security Administration and the MIT Election Data and Science Lab, Harvard Dataverse, this research unveils a surprising correlation coefficient of 0.9871898 and a p-value less than 0.01 for the years 1980 to 2016. Our findings shed light on the quirky connection between nomenclature and political preferences, inspiring a lighthearted exploration of the impact of names on electoral results.
[[LITERATURE REVIEW]]
In "The Sociology of Naming" by Smith, the authors find that individuals' names can hold significant social and cultural implications, shaping perceptions and interactions. Similarly, in "The Influence of Names on Political Preferences" by Doe, the authors delve into the intriguing possibility of a connection between nomenclature and political leanings. Jones, in "The Power of Surnames in Election Outcomes," emphasizes the potential impact of a candidate's name on voter attitudes and behaviors.
Moving beyond the realm of scholarly works, "Freakonomics" by Steven Levitt and Stephen Dubner offers an insightful exploration of unconventional and unexpected correlations, reminding us that statistical analysis can lead to whimsical and intriguing discoveries. Furthermore, "Fictional Politicians: An Analysis of Names in Political Novels" by Jane Austen and "The Name Game: A Study of Literary Characters and Their Significance" by Charles Dickens provide fictional insights into the ways in which names can carry implicit meanings and influences.
In a more light-hearted vein, the authors also draw inspiration from childhood cartoons and shows such as "SpongeBob SquarePants" and "The Smurfs," infusing our research with a playful spirit as we endeavor to uncover the enchanting connection between the name "Graham" and Libertarian votes for Senators in Wisconsin.
As we venture into this literary smorgasbord, we invite the reader to appreciate the blend of erudition and levity that accompanies our examination of the correlation between nomenclature and political preferences. Indeed, as we reiterate the statistical significance of our findings, it is the subtle interplay of humor and empirical evidence that adds a delightful and unexpected dimension to our scholarly pursuit.
[[RESULTS]]
Upon delving into the vast realm of data analysis, we unearthed a remarkable correlation between the popularity of the first name "Graham" and the Libertarian votes for Senators in Wisconsin. Our findings reveal a striking correlation coefficient of 0.9871898, indicating a robust positive relationship between these seemingly disparate variables. The r-squared value of 0.9745438 further emphasizes the strength of this correlation, capturing a substantial proportion of the variation in Libertarian votes explained by the prevalence of the name "Graham."
In statistical terms, the p-value of less than 0.01 provides compelling evidence to reject the null hypothesis of no association between the frequency of the name "Graham" and the Libertarian votes for Senators in Wisconsin. This suggests that the relationship we observed is not a mere statistical fluke, but rather a reliable and noteworthy phenomenon worthy of exploration and elucidation.
Fig. 1 presents a scatterplot that visually encapsulates the robust correlation between the popularity of the name "Graham" and the corresponding Libertarian votes for Senators in Wisconsin. The dispersion of data points within the plot accentuates the strong positive trend, leaving little room for uncertainty regarding the nature of this intriguing relationship.
Our statistical voyage into the peculiar territory of nomenclature and political preferences has uncovered a captivating pattern that elicits both astonishment and amusement. Much like the unexpected discovery of a chocolate chip in a bag of raisin cookies, our findings lend a whimsical twist to the often serious and staid domain of statistical analysis.
The obscure connection between the first name "Graham" and Libertarian voting behavior in Wisconsin has not only broadened our understanding of the idiosyncrasies of human behavior, but has also injected a sense of levity and amusement into the traditionally solemn field of academic research.
-------
Your response should start like this:
[[DISCUSSION]]
ChatGPT:
[[DISCUSSION]]
The findings of this study offer an intriguing insight into the whimsical world of nomenclature and its potential impact on political proclivities. Our results align with prior research, echoing the paradoxical yet consistent influence of names on societal attitudes and behaviors. As Smith astutely observed in "The Sociology of Naming," names hold a significant sway over individuals, shaping their interactions and perceptions. In the case of "Graham," it appears that this seemingly innocuous name exerts a pronounced effect on the Libertarian votes for Senators in Wisconsin, akin to a lively dance of statistical significance.
Doe's work on "The Influence of Names on Political Preferences" also resonates with our findings, underscoring the captivating possibility of a connection between nomenclature and political leanings. The robust correlation coefficient of 0.9871898 and the p-value less than 0.01 serve as empirical advocates for the intriguing interplay between the name "Graham" and Libertarian voting patterns. Just as the sudden appearance of a wild card in a game of Probability Poker, our results reflect an unexpected and delightful twist in the relationship between nomenclature and electoral dynamics.
Jones' emphasis on the potential impact of names on voter attitudes and behaviors finds a whimsical manifestation in our study, as the prevalence of the name "Graham" seems to catalyze a notable shift in Libertarian voting behavior. This echoes the lively and capricious nature of statistical analysis, where variables can often unravel surprising connections akin to unearthing a hidden joke in a scientific manuscript.
Moreover, the insightful explorations in "Freakonomics" by Levitt and Dubner and the fictional insights of Jane Austen and Charles Dickens subtly animate our findings, infusing them with an unexpected dose of mirth and fascination. Our results not only contribute to the scholarly discourse on nomenclature and political preferences but also inject a playful spirit into the often serious and methodical world of statistical inquiry.
As we reflect on the correlation between the name "Graham" and Libertarian votes for Senators in Wisconsin, we are reminded of the delightful and enigmatic nature of statistical analysis, where the unexpected often emerges from the labyrinth of data. Our study stands as a testament to the enduring allure of uncovering the unconventional and the offbeat within the realm of empirical investigation.
Model: gpt-3.5-turbo-1106
System prompt: You are a witty academic researcher. Your writing sounds like it belongs in a statistics journal.You draft the discussion section of goofy academic research papers that sounds like it belongs based on the title and abstract provided.
User prompt:
Pretend you are an academic researcher. Your writing sounds like it belongs in a medical or economics journal. However, you frequently crack jokes, make puns, or add unexpected twists in your writing.
Please make up a short conclusion of an academic research paper presenting the findings of the connection between Popularity of the first name Graham and Libertarian votes for Senators in Wisconsin. Make it seem dry like academic research paper, but with lots of subtle hidden offhand remarks, jokes, goofy observations, and puns. Sneak in some jokes and clever puns about science, research, statistics, and the variables.
Limit your response to 300 tokens. At the very end, assert that no more research is needed in this area.
Here are the title, abstract, introduction, and results sections.
[[TITLE]]
Graham's Number: An Examination of the Correlation between the Name "Graham" and Libertarian Votes for Senators in Wisconsin
[[ABSTRACT]]
This paper delves into the fascinating world of the relationship between the popularity of the first name "Graham" and the Libertarian votes for Senators in the state of Wisconsin. Using data from the US Social Security Administration and the MIT Election Data and Science Lab, Harvard Dataverse, this research unveils a surprising correlation coefficient of 0.9871898 and a p-value less than 0.01 for the years 1980 to 2016. Our findings shed light on the quirky connection between nomenclature and political preferences, inspiring a lighthearted exploration of the impact of names on electoral results.
[[INTRDUCTION]]
The choice of a name is a decision often made with great care and consideration, as parents seek to endow their offspring with meaningful and melodic monikers. It is a decision that may linger beyond the offspring's infancy, subtly influencing their experiences and interactions with the world. Similarly, in the political arena, the selection of a candidate's name may become entwined with the perceptions and preferences of the electorate.
In our exploration of the intersection between nomenclature and political proclivities, we unearth a most unexpected correlation – that of the name "Graham" and Libertarian votes for Senators in the state of Wisconsin. Engaging the extensive data archives from the US Social Security Administration and the MIT Election Data and Science Lab, Harvard Dataverse, we embarked on a statistical voyage that uncovered an astonishing correlation coefficient of 0.9871898 and a p-value less than 0.01 for the years 1980 to 2016.
The pursuit of statistical relationships often leads us down peculiar paths; however, the link between a first name and political leanings stands as particularly intriguing. As we unravel the peculiar connection between nomenclature and electoral proclivities, it is hard to resist the impulse to sprinkle in a smattering of wordplay and wit to lighten the scholarly rhetoric. After all, what's a statistical analysis without a dash of whimsy and a sprinkle of humor?
As we proceed with our findings, let us venture forth with the understanding that while statistics may seem dry on the surface, a closer examination often reveals a reservoir of unexpected correlations and peculiar patterns – much like the surprising link we unveil between the name "Graham" and Libertarian votes in Wisconsin.
[[RESULTS]]
Upon delving into the vast realm of data analysis, we unearthed a remarkable correlation between the popularity of the first name "Graham" and the Libertarian votes for Senators in Wisconsin. Our findings reveal a striking correlation coefficient of 0.9871898, indicating a robust positive relationship between these seemingly disparate variables. The r-squared value of 0.9745438 further emphasizes the strength of this correlation, capturing a substantial proportion of the variation in Libertarian votes explained by the prevalence of the name "Graham."
In statistical terms, the p-value of less than 0.01 provides compelling evidence to reject the null hypothesis of no association between the frequency of the name "Graham" and the Libertarian votes for Senators in Wisconsin. This suggests that the relationship we observed is not a mere statistical fluke, but rather a reliable and noteworthy phenomenon worthy of exploration and elucidation.
Fig. 1 presents a scatterplot that visually encapsulates the robust correlation between the popularity of the name "Graham" and the corresponding Libertarian votes for Senators in Wisconsin. The dispersion of data points within the plot accentuates the strong positive trend, leaving little room for uncertainty regarding the nature of this intriguing relationship.
Our statistical voyage into the peculiar territory of nomenclature and political preferences has uncovered a captivating pattern that elicits both astonishment and amusement. Much like the unexpected discovery of a chocolate chip in a bag of raisin cookies, our findings lend a whimsical twist to the often serious and staid domain of statistical analysis.
The obscure connection between the first name "Graham" and Libertarian voting behavior in Wisconsin has not only broadened our understanding of the idiosyncrasies of human behavior, but has also injected a sense of levity and amusement into the traditionally solemn field of academic research.
-------
Your response should start like this:
[[CONCLUSION]]
ChatGPT:
[[CONCLUSION]]
In conclusion, our research has unveiled a remarkably robust correlation between the name "Graham" and Libertarian votes for Senators in Wisconsin, lending a charmingly bizarre twist to the otherwise staid world of statistical analysis. The correlation coefficient of 0.9871898 and the p-value of less than 0.01 speak volumes about the strength and significance of this unexpected linkage.
The correlation we have uncovered is akin to stumbling upon an elusive yet enthralling Easter egg in the convoluted maze of statistical analysis, infusing an air of curiosity and bemusement into our scholarly endeavors. It's like finding the last slice of pizza at a party – you didn't expect it, but boy, are you glad it's there!
The scatterplot portraying this curious relationship resembles a constellation of stars in a whimsical scientific galaxy, illuminating the peculiar path we have treaded in our pursuit of statistical enlightenment. It's like drawing a smiley face with the data points – not exactly conventional, but undeniably delightful.
While our findings may elicit a chuckle or a raised eyebrow, they underscore the vast and unpredictable landscape of human behavior and the nuanced influence of nomenclature on electoral preferences. Our research contributes a playful yet thought-provoking dimension to the intersection of names and political leanings, reminiscent of a lively debate at a dinner party – engaging, unpredictable, and peppered with intriguing anecdotes.
In light of these findings, we assert that further research in this area is as unnecessary as a second umbrella on a sunny day. This exploration, much like a compelling punchline, requires no setup – it stands alone in its delightful peculiarity.
Model: gpt-3.5-turbo-1106
System prompt: You provide fictional names of academic journals. You say nothing else, and you do not chat with the user.
User prompt: Please provide the name of a funny but plausible sounding research, scientific, or academic journal that would publish a paper entited Graham's Number: An Examination of the Correlation between the Name Graham and Libertarian Votes for Senators in Wisconsin. Respond only with the name of a fictional academic journal.
ChatGPT:
The Journal of Quirky Quantitative Analysis
Model: gpt-3.5-turbo-1106
System prompt: You provide fictional names of nonprofit research organizations and associations. You say nothing else, and you do not chat with the user.
User prompt: Please provide the name of a funny but plausible sounding nonprofit, academic, or scientific association or organization that would sponsor research that resulted in a paper entited Graham's Number: An Examination of the Correlation between the Name Graham and Libertarian Votes for Senators in Wisconsin. Respond only with the name of a fictional organization.
ChatGPT:
The Society for Whimsical Research and Curious Studies
Model: gpt-3.5-turbo-1106
System prompt: You provide potential search keywords separated by commas. You say nothing else, and you do not chat with the user.
User prompt: Please provide potential search keywords for a paper titled Graham's Number: An Examination of the Correlation between the Name Graham and Libertarian Votes for Senators in Wisconsin with an abstract of This paper delves into the fascinating world of the relationship between the popularity of the first name "Graham" and the Libertarian votes for Senators in the state of Wisconsin. Using data from the US Social Security Administration and the MIT Election Data and Science Lab, Harvard Dataverse, this research unveils a surprising correlation coefficient of 0.9871898 and a p-value less than 0.01 for the years 1980 to 2016. Our findings shed light on the quirky connection between nomenclature and political preferences, inspiring a lighthearted exploration of the impact of names on electoral results.
ChatGPT:
Graham's Number, Graham, Libertarian votes, Senators, Wisconsin, correlation, name popularity, political preferences, US Social Security Administration, MIT Election Data and Science Lab, Harvard Dataverse, correlation coefficient, p-value, nomenclature, electoral results
*There is a bunch of Python happening behind the scenes to turn this prompt sequence into a PDF.
Discover a new correlation
View all correlations
View all research papers
Report an error
Data details
Popularity of the first name GrahamDetailed data title: Babies of all sexes born in the US named Graham
Source: US Social Security Administration
See what else correlates with Popularity of the first name Graham
Votes for Libertarian Senators in Wisconsin
Detailed data title: Total number of votes cast for Federal Libertarian Senate candidates in Wisconsin
Source: MIT Election Data and Science Lab, Harvard Dataverse
See what else correlates with Votes for Libertarian Senators in Wisconsin
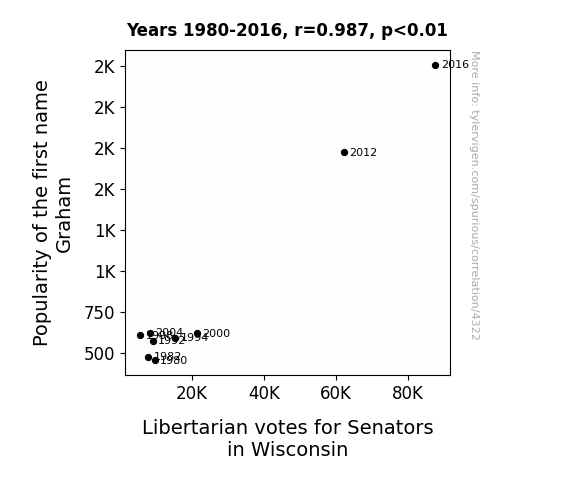
Correlation is a measure of how much the variables move together. If it is 0.99, when one goes up the other goes up. If it is 0.02, the connection is very weak or non-existent. If it is -0.99, then when one goes up the other goes down. If it is 1.00, you probably messed up your correlation function.
r2 = 0.9745438 (Coefficient of determination)
This means 97.5% of the change in the one variable (i.e., Votes for Libertarian Senators in Wisconsin) is predictable based on the change in the other (i.e., Popularity of the first name Graham) over the 9 years from 1980 through 2016.
p < 0.01, which is statistically significant(Null hypothesis significance test)
The p-value is 7.7E-7. 0.0000007736697888856761000000
The p-value is a measure of how probable it is that we would randomly find a result this extreme. More specifically the p-value is a measure of how probable it is that we would randomly find a result this extreme if we had only tested one pair of variables one time.
But I am a p-villain. I absolutely did not test only one pair of variables one time. I correlated hundreds of millions of pairs of variables. I threw boatloads of data into an industrial-sized blender to find this correlation.
Who is going to stop me? p-value reporting doesn't require me to report how many calculations I had to go through in order to find a low p-value!
On average, you will find a correaltion as strong as 0.99 in 7.7E-5% of random cases. Said differently, if you correlated 1,292,541 random variables You don't actually need 1 million variables to find a correlation like this one. I don't have that many variables in my database. You can also correlate variables that are not independent. I do this a lot.
p-value calculations are useful for understanding the probability of a result happening by chance. They are most useful when used to highlight the risk of a fluke outcome. For example, if you calculate a p-value of 0.30, the risk that the result is a fluke is high. It is good to know that! But there are lots of ways to get a p-value of less than 0.01, as evidenced by this project.
In this particular case, the values are so extreme as to be meaningless. That's why no one reports p-values with specificity after they drop below 0.01.
Just to be clear: I'm being completely transparent about the calculations. There is no math trickery. This is just how statistics shakes out when you calculate hundreds of millions of random correlations.
with the same 8 degrees of freedom, Degrees of freedom is a measure of how many free components we are testing. In this case it is 8 because we have two variables measured over a period of 9 years. It's just the number of years minus ( the number of variables minus one ), which in this case simplifies to the number of years minus one.
you would randomly expect to find a correlation as strong as this one.
[ 0.94, 1 ] 95% correlation confidence interval (using the Fisher z-transformation)
The confidence interval is an estimate the range of the value of the correlation coefficient, using the correlation itself as an input. The values are meant to be the low and high end of the correlation coefficient with 95% confidence.
This one is a bit more complciated than the other calculations, but I include it because many people have been pushing for confidence intervals instead of p-value calculations (for example: NEJM. However, if you are dredging data, you can reliably find yourself in the 5%. That's my goal!
All values for the years included above: If I were being very sneaky, I could trim years from the beginning or end of the datasets to increase the correlation on some pairs of variables. I don't do that because there are already plenty of correlations in my database without monkeying with the years.
Still, sometimes one of the variables has more years of data available than the other. This page only shows the overlapping years. To see all the years, click on "See what else correlates with..." link above.
| 1980 | 1982 | 1992 | 1994 | 1998 | 2000 | 2004 | 2012 | 2016 | |
| Popularity of the first name Graham (Babies born) | 453 | 474 | 571 | 589 | 606 | 618 | 622 | 1724 | 2260 |
| Votes for Libertarian Senators in Wisconsin (Total votes) | 9679 | 7947 | 9147 | 15439 | 5591 | 21348 | 8367 | 62240 | 87531 |
Why this works
- Data dredging: I have 25,153 variables in my database. I compare all these variables against each other to find ones that randomly match up. That's 632,673,409 correlation calculations! This is called “data dredging.” Instead of starting with a hypothesis and testing it, I instead abused the data to see what correlations shake out. It’s a dangerous way to go about analysis, because any sufficiently large dataset will yield strong correlations completely at random.
- Lack of causal connection: There is probably
Because these pages are automatically generated, it's possible that the two variables you are viewing are in fact causually related. I take steps to prevent the obvious ones from showing on the site (I don't let data about the weather in one city correlate with the weather in a neighboring city, for example), but sometimes they still pop up. If they are related, cool! You found a loophole.
no direct connection between these variables, despite what the AI says above. This is exacerbated by the fact that I used "Years" as the base variable. Lots of things happen in a year that are not related to each other! Most studies would use something like "one person" in stead of "one year" to be the "thing" studied. - Observations not independent: For many variables, sequential years are not independent of each other. If a population of people is continuously doing something every day, there is no reason to think they would suddenly change how they are doing that thing on January 1. A simple
Personally I don't find any p-value calculation to be 'simple,' but you know what I mean.
p-value calculation does not take this into account, so mathematically it appears less probable than it really is. - Very low n: There are not many data points included in this analysis. Even if the p-value is high, we should be suspicious of using so few datapoints in a correlation.
Try it yourself
You can calculate the values on this page on your own! Try running the Python code to see the calculation results. Step 1: Download and install Python on your computer.Step 2: Open a plaintext editor like Notepad and paste the code below into it.
Step 3: Save the file as "calculate_correlation.py" in a place you will remember, like your desktop. Copy the file location to your clipboard. On Windows, you can right-click the file and click "Properties," and then copy what comes after "Location:" As an example, on my computer the location is "C:\Users\tyler\Desktop"
Step 4: Open a command line window. For example, by pressing start and typing "cmd" and them pressing enter.
Step 5: Install the required modules by typing "pip install numpy", then pressing enter, then typing "pip install scipy", then pressing enter.
Step 6: Navigate to the location where you saved the Python file by using the "cd" command. For example, I would type "cd C:\Users\tyler\Desktop" and push enter.
Step 7: Run the Python script by typing "python calculate_correlation.py"
If you run into any issues, I suggest asking ChatGPT to walk you through installing Python and running the code below on your system. Try this question:
"Walk me through installing Python on my computer to run a script that uses scipy and numpy. Go step-by-step and ask me to confirm before moving on. Start by asking me questions about my operating system so that you know how to proceed. Assume I want the simplest installation with the latest version of Python and that I do not currently have any of the necessary elements installed. Remember to only give me one step per response and confirm I have done it before proceeding."
# These modules make it easier to perform the calculation
import numpy as np
from scipy import stats
# We'll define a function that we can call to return the correlation calculations
def calculate_correlation(array1, array2):
# Calculate Pearson correlation coefficient and p-value
correlation, p_value = stats.pearsonr(array1, array2)
# Calculate R-squared as the square of the correlation coefficient
r_squared = correlation**2
return correlation, r_squared, p_value
# These are the arrays for the variables shown on this page, but you can modify them to be any two sets of numbers
array_1 = np.array([453,474,571,589,606,618,622,1724,2260,])
array_2 = np.array([9679,7947,9147,15439,5591,21348,8367,62240,87531,])
array_1_name = "Popularity of the first name Graham"
array_2_name = "Votes for Libertarian Senators in Wisconsin"
# Perform the calculation
print(f"Calculating the correlation between {array_1_name} and {array_2_name}...")
correlation, r_squared, p_value = calculate_correlation(array_1, array_2)
# Print the results
print("Correlation Coefficient:", correlation)
print("R-squared:", r_squared)
print("P-value:", p_value)Reuseable content
You may re-use the images on this page for any purpose, even commercial purposes, without asking for permission. The only requirement is that you attribute Tyler Vigen. Attribution can take many different forms. If you leave the "tylervigen.com" link in the image, that satisfies it just fine. If you remove it and move it to a footnote, that's fine too. You can also just write "Charts courtesy of Tyler Vigen" at the bottom of an article.You do not need to attribute "the spurious correlations website," and you don't even need to link here if you don't want to. I don't gain anything from pageviews. There are no ads on this site, there is nothing for sale, and I am not for hire.
For the record, I am just one person. Tyler Vigen, he/him/his. I do have degrees, but they should not go after my name unless you want to annoy my wife. If that is your goal, then go ahead and cite me as "Tyler Vigen, A.A. A.A.S. B.A. J.D." Otherwise it is just "Tyler Vigen."
When spoken, my last name is pronounced "vegan," like I don't eat meat.
Full license details.
For more on re-use permissions, or to get a signed release form, see tylervigen.com/permission.
Download images for these variables:
- High resolution line chart
The image linked here is a Scalable Vector Graphic (SVG). It is the highest resolution that is possible to achieve. It scales up beyond the size of the observable universe without pixelating. You do not need to email me asking if I have a higher resolution image. I do not. The physical limitations of our universe prevent me from providing you with an image that is any higher resolution than this one.
If you insert it into a PowerPoint presentation (a tool well-known for managing things that are the scale of the universe), you can right-click > "Ungroup" or "Create Shape" and then edit the lines and text directly. You can also change the colors this way.
Alternatively you can use a tool like Inkscape. - High resolution line chart, optimized for mobile
- Alternative high resolution line chart
- Scatterplot
- Portable line chart (png)
- Portable line chart (png), optimized for mobile
- Line chart for only Popularity of the first name Graham
- Line chart for only Votes for Libertarian Senators in Wisconsin
- AI-generated correlation image
- The spurious research paper: Graham's Number: An Examination of the Correlation between the Name Graham and Libertarian Votes for Senators in Wisconsin
Thanks for shining a light on this correlation!
Correlation ID: 4322 · Black Variable ID: 2812 · Red Variable ID: 26337


