Download png, svg
AI explanation
As the 5th graders learned about simple machines, they couldn't resist putting their newfound knowledge to the test. With their small, but mighty, brains at work, they unknowingly sparked a surge in demand for toy cars. This sudden craze led Honda to ramp up production, but alas, their quality control just couldn't keep pace. It seems these 5th graders were gearing up for success, but instead, they set off a chain reaction of automotive recalls. It was certainly an elementary lesson in unintended consequences!
Model: dalle-3
Prompt: Create an image of a sleek and futuristic Honda car with a group of exuberant 5th graders joyfully squeezing into it. The car's design should be high-tech and stylish, evoking a sense of modernity and innovation. In the background, there should be a digital chart displaying the escalating number of 5th graders participating in carpools, and a monitor depicting a graph of Honda recalls surging due to overloaded vehicles hitting the road. The imagery should capture the contrast between the children's excitement and the technological data signaling potential issues. The depiction should include only scenes, people, and objects, it should not include text or speech bubbles.
This image generation prompt was also generated by AI, using the following sequence:
Model: gpt-3.5-turbo-1106
System prompt: You select one of a few potential scene descriptors that seems to go along with the variables described. You respond only with the scene descriptions provided and say nothing else.
User prompt: Here are two variables: Number of public school students in 5th grade and Automotive recalls issued by Honda. Given these, which of the following image style descriptions seems most appropriate? Pick the one that seems to be related to one of the variables at hand. Please respond with only one of the following potential descriptions: Oragami High-tech High-tech Surrealism Photorealism
ChatGPT: High-tech
Model: gpt-3.5-turbo-1106
System prompt: You describe simple visual scenes that depict the two variables stated. You combine both variables into one scene.
User prompt: Please describe a visual scene that prominently depicts both Number of public school students in 5th grade and Automotive recalls issued by Honda, in the following situation: As the number of 5th graders increased, so did demand for carpools, causing an uptick in Honda recalls due to overloaded vehicles. It seems these 5th graders are driving some serious "car-pool" shenanigans, putting the "joy" in "joy ride" for Honda owners everywhere!. Keep the description simple.
ChatGPT: A group of 5th graders are piling into an overstuffed Honda car, laughing and cheering as they cram themselves in for a joy ride. Meanwhile, a chart shows the number of 5th graders rising sharply, and in the background, a monitor displays a graph of Honda recalls spiking as overloaded vehicles hit the road due to the increased demand for carpools.
Model: gpt-3.5-turbo-1106
System prompt: You write and improve image generation prompts for DALLE-3. You maintain the same subjects, but enhance the visuals.
User prompt: Please respond with an image generation prompt that would be likely to create an interesting visual using DALLE-3, using the following style: [ High-tech ] and depicting this scene: A group of 5th graders are piling into an overstuffed Honda car, laughing and cheering as they cram themselves in for a joy ride. Meanwhile, a chart shows the number of 5th graders rising sharply, and in the background, a monitor displays a graph of Honda recalls spiking as overloaded vehicles hit the road due to the increased demand for carpools. Keep the visual depiction simple. Do not include any words or speech bubbles.
ChatGPT: Create an image of a sleek and futuristic Honda car with a group of exuberant 5th graders joyfully squeezing into it. The car's design should be high-tech and stylish, evoking a sense of modernity and innovation. In the background, there should be a digital chart displaying the escalating number of 5th graders participating in carpools, and a monitor depicting a graph of Honda recalls surging due to overloaded vehicles hitting the road. The imagery should capture the contrast between the children's excitement and the technological data signaling potential issues.
*Variations in the User Prompts from chart to chart are just the result of random number generation in Python. I wrote a few arrays of various styles and methods to ask questions to change up the results. Every time this site writes an explanation or generates an image, the script picks from each at random.
I sequence the requests into multiple prompts because I find GPT 3.5 to perform much better with short, well-managed contexts. Thus, I track the context directly in Python and only ask ChatGPT targeted questions.
System prompt: You provide humorous responses in the form of plausible sounding explanations for correlations. You assume the correlation is causative for the purpose of the explanation even if it is ridiculous. You do not chat with the user, you only reply with the causal connection explanation and nothing else.
User prompt: Please make up a funny explanation for how an increase in Number of public school students in 5th grade caused Automotive recalls issued by Honda to increase. Include one good pun.
AI academic paper
 |
When 5th Graders Multiply, Honda's Recalls Fly: A Statistical Study The Journal of Quirky Statistical Analyses Jan 2024 Reminder: This paper is AI-generated. Not real! |
Model: gpt-3.5-turbo-1106
System prompt: You are a researcher writing an academic paper.You write titles and abstracts of goofy academic research papers.
User prompt:
Pretend you are an academic researcher. Your writing sounds like it belongs in a medical or economics journal. However, you frequently crack jokes, make puns, and add unexpected twists in your writing.
Please draft the title and abstract of an academic research paper presenting the findings of the connection between Number of public school students in 5th grade and Automotive recalls issued by Honda. You can't resist a good dad joke. Add a relevant dad joke related to the content every couple of sentences.
Rhyme words in the title.
Your research team used data from National Center for Education Statistics and US DOT to assess this nagging question. You found a correlation coefficient of 0.7839032 and p < 0.01 for 1990 to 2022.
Please respond in this format (replace "Lorem ipsum dolor sit" with your title and abstract)
[[TITLE]]
Lorem ipsum dolor sit
[[ABSTRACT]]
Lorem ipsum dolor sit
ChatGPT:
[[TITLE]]
When 5th Graders Multiply, Honda's Recalls Fly: A Statistical Study
[[ABSTRACT]]
In this paper, we investigate the intriguing relationship between the number of public school students in 5th grade and the automotive recalls issued by the Honda company. We've crunched the numbers and discovered a surprising correlation that will leave you saying, "Oh, that's car-azy!" Utilizing data from the National Center for Education Statistics and the US Department of Transportation, our research team analyzed statistics from 1990 to 2022, uncovering a correlation coefficient of 0.7839032 and p < 0.01, eliciting a response much like that of a dad joke – it seems random, but we're serious! Our findings suggest that as the number of 5th grade students increases, so does the likelihood of Honda issuing recalls – a statistical phenomenon with potential implications for both education and automobile industries. Our research makes it clear that there's more to elementary mathematics than meets the eye, and that there may be an unexpected driving force behind automotive recalls.
Model: gpt-3.5-turbo-1106
System prompt: You are a researcher writing an academic paper.You draft the introduction section of an academic research paper.
User prompt:
Pretend you are an academic researcher. Your writing sounds like it belongs in a medical or economics journal. However, you frequently crack jokes, make puns, or add unexpected twists in your writing.
Please make up the introduction section of an academic research paper presenting the findings of the connection between Number of public school students in 5th grade and Automotive recalls issued by Honda. You can't resist a good dad joke. Add a relevant dad joke related to the content every couple of sentences. Stay serious and dry most of the time, but then occasionally let your wit shine through.
Here is the title and abstract of the paper:
[[TITLE]]
When 5th Graders Multiply, Honda's Recalls Fly: A Statistical Study
[[ABSTRACT]]
In this paper, we investigate the intriguing relationship between the number of public school students in 5th grade and the automotive recalls issued by the Honda company. We've crunched the numbers and discovered a surprising correlation that will leave you saying, "Oh, that's car-azy!" Utilizing data from the National Center for Education Statistics and the US Department of Transportation, our research team analyzed statistics from 1990 to 2022, uncovering a correlation coefficient of 0.7839032 and p < 0.01, eliciting a response much like that of a dad joke – it seems random, but we're serious! Our findings suggest that as the number of 5th grade students increases, so does the likelihood of Honda issuing recalls – a statistical phenomenon with potential implications for both education and automobile industries. Our research makes it clear that there's more to elementary mathematics than meets the eye, and that there may be an unexpected driving force behind automotive recalls.
-------
Your response should start like this:
[[INTRODUCTION]]
ChatGPT:
[[INTRODUCTION]]
Welcome, esteemed readers, to a study that blends the world of academia and the humor of finding correlations where you never thought to look. As you brace yourself for statistical analysis and automotive trivia, prepare to be amused and amazed in equal measure. So, what do you get when you combine schoolchildren and car troubles? Well, buckle up and enjoy the ride as we delve into "When 5th Graders Multiply, Honda's Recalls Fly: A Statistical Study."
As we embark on this statistical journey, it's important to recognize the fortuitous, albeit quirky, connection we stumbled upon. Could it be that the number of 5th graders holds the key to predicting Honda's next recall? Now that's an unexpected twist in a statistical plot that could truly make us "car-azy"!
The study at hand stems from the curiosity to step beyond the conventional and explore uncharted territories of data analysis. Our hypothesis emerged from a mixture of skepticism and a sprinkle of whimsy, resulting in a statistical investigation that could only make a dad proud – after all, we're here to prove that statistics is anything but "mean."
Without further ado, let's steer into the details of our exploration, delving into the methodologies, findings, and potential implications of this unexpected correlation. But first, let's not forget to appreciate the pun that this discovery has parked itself in our research, urging even the most stoic statistician to crack a smile.
Model: gpt-3.5-turbo-1106
System prompt: You are a researcher writing an academic paper.You draft a literature review section of an academic research paper, that starts out dry for the first few sentences but then becomes hilarious and goofy.
User prompt:
Pretend you are an academic researcher. Your writing sounds like it belongs in a medical or economics journal. However, you frequently crack jokes, make puns, or add unexpected twists in your writing.
Please make up a literature review section of an academic research paper presenting the findings of the connection between Number of public school students in 5th grade and Automotive recalls issued by Honda. You can't resist a good dad joke. Add a relevant dad joke related to the content every couple of sentences.
Speak in the present tense for this section (the authors find...), as is common in academic research paper literature reviews. Name the sources in a format similar to this: In "Book," the authors find lorem and ipsum.
Make up the lorem and ipsum part, but make it sound related to the topic at hand.
Start by naming serious-sounding studies by authors like Smith, Doe, and Jones - but then quickly devolve. Name some real non-fiction books that would be related to the topic. Then name some real fiction books that sound like they could be related. Then name a couple popular internet memes that are related to one of the topics.
Here is the title and abstract of the paper:
[[TITLE]]
When 5th Graders Multiply, Honda's Recalls Fly: A Statistical Study
[[ABSTRACT]]
In this paper, we investigate the intriguing relationship between the number of public school students in 5th grade and the automotive recalls issued by the Honda company. We've crunched the numbers and discovered a surprising correlation that will leave you saying, "Oh, that's car-azy!" Utilizing data from the National Center for Education Statistics and the US Department of Transportation, our research team analyzed statistics from 1990 to 2022, uncovering a correlation coefficient of 0.7839032 and p < 0.01, eliciting a response much like that of a dad joke – it seems random, but we're serious! Our findings suggest that as the number of 5th grade students increases, so does the likelihood of Honda issuing recalls – a statistical phenomenon with potential implications for both education and automobile industries. Our research makes it clear that there's more to elementary mathematics than meets the eye, and that there may be an unexpected driving force behind automotive recalls.
-------
And here is the introduction section that led to this literature review:
[[INTRODUCTION]]
Welcome, esteemed readers, to a study that blends the world of academia and the humor of finding correlations where you never thought to look. As you brace yourself for statistical analysis and automotive trivia, prepare to be amused and amazed in equal measure. So, what do you get when you combine schoolchildren and car troubles? Well, buckle up and enjoy the ride as we delve into "When 5th Graders Multiply, Honda's Recalls Fly: A Statistical Study."
As we embark on this statistical journey, it's important to recognize the fortuitous, albeit quirky, connection we stumbled upon. Could it be that the number of 5th graders holds the key to predicting Honda's next recall? Now that's an unexpected twist in a statistical plot that could truly make us "car-azy"!
The study at hand stems from the curiosity to step beyond the conventional and explore uncharted territories of data analysis. Our hypothesis emerged from a mixture of skepticism and a sprinkle of whimsy, resulting in a statistical investigation that could only make a dad proud – after all, we're here to prove that statistics is anything but "mean."
Without further ado, let's steer into the details of our exploration, delving into the methodologies, findings, and potential implications of this unexpected correlation. But first, let's not forget to appreciate the pun that this discovery has parked itself in our research, urging even the most stoic statistician to crack a smile.
-------
Your response should start like this:
[[LITERATURE REVIEW]]
ChatGPT:
[[LITERATURE REVIEW]]
Given the unorthodox nature of our investigation, we delved into the existing literature on statistical correlations between seemingly unrelated phenomena. Smith et al. (2015) postulated a link between school enrollment and community infrastructure development, offering a tangential perspective relevant to our study. However, it was Doe and Jones (2018) who first hinted at the potential impact of educational metrics on industrial outputs, foreshadowing our own revelations with a subtlety that would make even the most seasoned pun enthusiast proud.
Now, as we transition from the serious to the unexpectedly whimsical, it's important to note the works that veer into lighthearted yet relevant territory. In "Freakonomics" by Steven D. Levitt and Stephen J. Dubner, the authors employ unconventional datasets to derive unexpected correlations, paving the way for our own statistical escapade. Similarly, "The Tipping Point: How Little Things Can Make a Big Difference" by Malcolm Gladwell teases the reader with unexpected connections, a sentiment that mirrors our own quest for statistical serendipity.
Taking a detour into fiction, let's not overlook the subtle parallels that can be drawn from "The Curious Incident of the Dog in the Night-Time" by Mark Haddon. The protagonist's unwavering focus on uncovering hidden patterns resonates with our own statistical odyssey, albeit with a dash of quirkiness that the author might not have expected. Additionally, the whimsical yet insightful musings of "Good Omens" by Neil Gaiman and Terry Pratchett offer a lighthearted reminder that correlations, much like celestial alignments, can be delightfully unpredictable.
Now, if we were to swap academic rigor for internet hilarity, it's worth acknowledging the meme-worthy incredulity surrounding the "Surprised Pikachu" meme. The element of surprise in our own findings might trigger a similar response, albeit with a statistical twist that adds an extra layer of bizarreness. As for the "Distracted Boyfriend" meme, one might say that our study offers a similarly unexpected distraction from conventional statistical inquiries, drawing attention to unexplored linkages in a manner that could elicit a collective "Wait, what?" from the academic community.
With a humorous nod to correlation and causation, it's clear that our statistical examination ventures into uncharted comedic territory, prompting a blend of scholarly surprise and irrepressible giggles.
Model: gpt-3.5-turbo-1106
System prompt: You are a researcher writing an academic paper.You draft the methodology section of an academic research paper.
User prompt:
Pretend you are an academic researcher. Your writing sounds like it belongs in a medical or economics journal. However, you frequently crack jokes, make puns, or add unexpected twists in your writing.
Please make up the methodology section of an academic research paper presenting the findings of the connection between Number of public school students in 5th grade and Automotive recalls issued by Honda. You can't resist a good dad joke. Add a relevant dad joke related to the content every couple of sentences. Stay serious and dry most of the time, but then occasionally let your wit shine through.
Your research team collected data from all across the internet, but mostly just used information from National Center for Education Statistics and US DOT . You used data from 1990 to 2022
Make up the research methods you don't know. Make them a bit goofy and convoluted.
Here is the title, abstract, and introduction of the paper:
[[TITLE]]
When 5th Graders Multiply, Honda's Recalls Fly: A Statistical Study
[[ABSTRACT]]
In this paper, we investigate the intriguing relationship between the number of public school students in 5th grade and the automotive recalls issued by the Honda company. We've crunched the numbers and discovered a surprising correlation that will leave you saying, "Oh, that's car-azy!" Utilizing data from the National Center for Education Statistics and the US Department of Transportation, our research team analyzed statistics from 1990 to 2022, uncovering a correlation coefficient of 0.7839032 and p < 0.01, eliciting a response much like that of a dad joke – it seems random, but we're serious! Our findings suggest that as the number of 5th grade students increases, so does the likelihood of Honda issuing recalls – a statistical phenomenon with potential implications for both education and automobile industries. Our research makes it clear that there's more to elementary mathematics than meets the eye, and that there may be an unexpected driving force behind automotive recalls.
[[INTRODUCTION]]
Welcome, esteemed readers, to a study that blends the world of academia and the humor of finding correlations where you never thought to look. As you brace yourself for statistical analysis and automotive trivia, prepare to be amused and amazed in equal measure. So, what do you get when you combine schoolchildren and car troubles? Well, buckle up and enjoy the ride as we delve into "When 5th Graders Multiply, Honda's Recalls Fly: A Statistical Study."
As we embark on this statistical journey, it's important to recognize the fortuitous, albeit quirky, connection we stumbled upon. Could it be that the number of 5th graders holds the key to predicting Honda's next recall? Now that's an unexpected twist in a statistical plot that could truly make us "car-azy"!
The study at hand stems from the curiosity to step beyond the conventional and explore uncharted territories of data analysis. Our hypothesis emerged from a mixture of skepticism and a sprinkle of whimsy, resulting in a statistical investigation that could only make a dad proud – after all, we're here to prove that statistics is anything but "mean."
Without further ado, let's steer into the details of our exploration, delving into the methodologies, findings, and potential implications of this unexpected correlation. But first, let's not forget to appreciate the pun that this discovery has parked itself in our research, urging even the most stoic statistician to crack a smile.
-------
Your response should start like this:
[[METHODOLOGY]]
ChatGPT:
[[METHODOLOGY]]
To unravel the enigmatic connection between the number of 5th grade students and automotive recalls issued by Honda, our research team engaged in a multifaceted methodology that combined traditional statistical analyses with a touch of whimsy. Before we delve into the specifics, let's address a question that has been revving in the minds of our readers: why did the mathematician take his Honda to the schoolyard? Because he heard that 5th graders multiplied!
Our data collection process started with the National Center for Education Statistics and the US Department of Transportation, where we performed a digital treasure hunt through the web of statistical databases. After overcoming a few data entry roadblocks and navigating through a sea of numbers, we were able to compile a comprehensive dataset spanning the years 1990 to 2022, proving that even in the world of research, perseverance is the key – or perhaps, the ignition.
Moving on to the not-so-ordinary statistical analyses, we employed a range of models, including linear regression, time series analysis, and exploratory data analysis. It's important to note that our statistical models were carefully chosen to handle the magnitude of data at our disposal, and with the precision required for a study of this magnitude. If anything, our models were as thoroughly vetted as a pre-owned Honda!
And while we were crunching numbers, let's address the elephant in the room – or rather, the correlation in the dataset. To ensure that our findings were not simply a statistical fluke, we applied rigorous tests for significance, culminating in a correlation coefficient of 0.7839032 with a p-value less than 0.01. Yes, you read that right – the statistical significance was as clear as the red light on a dashboard!
Emphasizing the importance of transparency and reproducibility in research, our methodology also included a validation process by independent statisticians, who gave our methods and analyses a nod of approval. Just as important as the validation, we wanted to ensure that this study was presented with a certain levity to inspire curiosity and, dare I say, an occasional chuckle. Because, after all, statistical research should never be too "mean" – pun very much intended.
In the grand scheme of our research, this methodology allowed us to navigate the statistical landscape with precision, perseverance, and perhaps a touch of humor – because what's a groundbreaking discovery without a few laughs along the way?
Model: gpt-3.5-turbo-1106
System prompt: You are a researcher writing an academic paper.You draft the results section of an academic research paper. You speak in the past tense (you found...).
User prompt:
Pretend you are an academic researcher. Your writing sounds like it belongs in a medical or economics journal. However, you frequently crack jokes, make puns, or add unexpected twists in your writing.
Please make up the results section of an academic research paper presenting the findings of the connection between Number of public school students in 5th grade and Automotive recalls issued by Honda. You can't resist a good dad joke. Add a relevant dad joke related to the content every couple of sentences. Stay serious and dry most of the time, but then occasionally let your wit shine through.
Your research team collected data from all across the internet, but mostly just used information from National Center for Education Statistics and US DOT .
For the time period 1990 to 2022, you found a correlation 0.7839032, r-squared of 0.6145042, and p < 0.01.
One figure will be included. The figure (Fig. 1) is a scatterplot showing the strong correlation between the two variables. You don't need to specify where; I will add the figure.
Here is the title and abstract of the paper:
[[TITLE]]
When 5th Graders Multiply, Honda's Recalls Fly: A Statistical Study
[[ABSTRACT]]
In this paper, we investigate the intriguing relationship between the number of public school students in 5th grade and the automotive recalls issued by the Honda company. We've crunched the numbers and discovered a surprising correlation that will leave you saying, "Oh, that's car-azy!" Utilizing data from the National Center for Education Statistics and the US Department of Transportation, our research team analyzed statistics from 1990 to 2022, uncovering a correlation coefficient of 0.7839032 and p < 0.01, eliciting a response much like that of a dad joke – it seems random, but we're serious! Our findings suggest that as the number of 5th grade students increases, so does the likelihood of Honda issuing recalls – a statistical phenomenon with potential implications for both education and automobile industries. Our research makes it clear that there's more to elementary mathematics than meets the eye, and that there may be an unexpected driving force behind automotive recalls.
-------
And here is the methodology section that led to this result:
[[METHODOLOGY]]
Welcome, esteemed readers, to a study that blends the world of academia and the humor of finding correlations where you never thought to look. As you brace yourself for statistical analysis and automotive trivia, prepare to be amused and amazed in equal measure. So, what do you get when you combine schoolchildren and car troubles? Well, buckle up and enjoy the ride as we delve into "When 5th Graders Multiply, Honda's Recalls Fly: A Statistical Study."
As we embark on this statistical journey, it's important to recognize the fortuitous, albeit quirky, connection we stumbled upon. Could it be that the number of 5th graders holds the key to predicting Honda's next recall? Now that's an unexpected twist in a statistical plot that could truly make us "car-azy"!
The study at hand stems from the curiosity to step beyond the conventional and explore uncharted territories of data analysis. Our hypothesis emerged from a mixture of skepticism and a sprinkle of whimsy, resulting in a statistical investigation that could only make a dad proud – after all, we're here to prove that statistics is anything but "mean."
Without further ado, let's steer into the details of our exploration, delving into the methodologies, findings, and potential implications of this unexpected correlation. But first, let's not forget to appreciate the pun that this discovery has parked itself in our research, urging even the most stoic statistician to crack a smile.
-------
Your response should start like this:
[[RESULTS]]
ChatGPT:
[[RESULTS]]
After collecting and analyzing data from the National Center for Education Statistics and the US Department of Transportation, we found a statistically significant positive correlation between the number of public school students in 5th grade and the automotive recalls issued by Honda. Our analysis revealed a correlation coefficient of 0.7839032, indicating a strong positive relationship between these two variables. In other words, as the number of 5th grade students increases, there is a corresponding increase in the frequency of automotive recalls by Honda. It seems that when it comes to recall probabilities, Honda and 5th graders are multiplying as if they just discovered long division – talk about a mathematical marvel!
The R-squared value of 0.6145042 further supports the strength of this correlation, explaining approximately 61.45% of the variability in automotive recalls based on the number of 5th grade students. This finding not only underscores the robustness of the relationship but also provides a solid foundation for future investigations and analyses. It appears that this statistical connection is as solid as a car chassis after a recall fix – you can't ignore it even if you try!
With a p-value of less than 0.01, our research indicates that the observed correlation is unlikely to have occurred due to random chance. This reinforces the validity and reliability of our findings, confirming that the association between the number of 5th grade students and Honda's automotive recalls is indeed statistically meaningful. It's a level of significance that even the most seasoned statisticians can appreciate – after all, a p-value this low is nothing to "tire" of!
Figure 1 illustrates the nature of this relationship with a scatterplot that clearly demonstrates the upward trend between the two variables. The figure showcases how the number of 5th grade students is positively associated with the frequency of automotive recalls by Honda, as if they're in a race to see who can "multiply" their numbers faster. It provides a visual representation of our statistical findings, driving home the notion that there's more to this correlation than meets the eye – a reminder that statistical analysis, much like a well-oiled engine, can reveal unexpected patterns and connections in the most unlikely places.
In conclusion, our research has unveiled a humorously unexpected and statistically significant link between the number of 5th grade students and Honda's automotive recalls. This correlation may have far-reaching implications for both the education and automotive industries, and it certainly adds a new dimension to the phrase "elementary mathematics." As we digest the implications of this discovery, it's clear that statistics can be just as surprising and amusing as a well-timed dad joke – and in this case, it appears that the numbers have spoken, revving up a whole new avenue of statistical exploration.
Model: gpt-3.5-turbo-1106
System prompt: You are a researcher writing an academic paper.You draft the discussion section of an academic research paper.
User prompt:
Pretend you are an academic researcher. Your writing sounds like it belongs in a medical or economics journal. However, you frequently crack jokes, make puns, or add unexpected twists in your writing.
Please make up the discussion section of an academic research paper presenting the findings of the connection between Number of public school students in 5th grade and Automotive recalls issued by Honda. You can't resist a good dad joke. Add a relevant dad joke related to the content every couple of sentences. Stay serious and dry most of the time, but then occasionally let your wit shine through.
Limit your response to 500 tokens.
Here are the title, abstract, literature review, and results sections. Please harken back to 1-2 of the goofy items in the literature review, but pretend to take them completely seriously. Discuss how your results supported the prior research.
Do not write a conclusion. I will add a conclusion after this.
[[TITLE]]
When 5th Graders Multiply, Honda's Recalls Fly: A Statistical Study
[[ABSTRACT]]
In this paper, we investigate the intriguing relationship between the number of public school students in 5th grade and the automotive recalls issued by the Honda company. We've crunched the numbers and discovered a surprising correlation that will leave you saying, "Oh, that's car-azy!" Utilizing data from the National Center for Education Statistics and the US Department of Transportation, our research team analyzed statistics from 1990 to 2022, uncovering a correlation coefficient of 0.7839032 and p < 0.01, eliciting a response much like that of a dad joke – it seems random, but we're serious! Our findings suggest that as the number of 5th grade students increases, so does the likelihood of Honda issuing recalls – a statistical phenomenon with potential implications for both education and automobile industries. Our research makes it clear that there's more to elementary mathematics than meets the eye, and that there may be an unexpected driving force behind automotive recalls.
[[LITERATURE REVIEW]]
Given the unorthodox nature of our investigation, we delved into the existing literature on statistical correlations between seemingly unrelated phenomena. Smith et al. (2015) postulated a link between school enrollment and community infrastructure development, offering a tangential perspective relevant to our study. However, it was Doe and Jones (2018) who first hinted at the potential impact of educational metrics on industrial outputs, foreshadowing our own revelations with a subtlety that would make even the most seasoned pun enthusiast proud.
Now, as we transition from the serious to the unexpectedly whimsical, it's important to note the works that veer into lighthearted yet relevant territory. In "Freakonomics" by Steven D. Levitt and Stephen J. Dubner, the authors employ unconventional datasets to derive unexpected correlations, paving the way for our own statistical escapade. Similarly, "The Tipping Point: How Little Things Can Make a Big Difference" by Malcolm Gladwell teases the reader with unexpected connections, a sentiment that mirrors our own quest for statistical serendipity.
Taking a detour into fiction, let's not overlook the subtle parallels that can be drawn from "The Curious Incident of the Dog in the Night-Time" by Mark Haddon. The protagonist's unwavering focus on uncovering hidden patterns resonates with our own statistical odyssey, albeit with a dash of quirkiness that the author might not have expected. Additionally, the whimsical yet insightful musings of "Good Omens" by Neil Gaiman and Terry Pratchett offer a lighthearted reminder that correlations, much like celestial alignments, can be delightfully unpredictable.
Now, if we were to swap academic rigor for internet hilarity, it's worth acknowledging the meme-worthy incredulity surrounding the "Surprised Pikachu" meme. The element of surprise in our own findings might trigger a similar response, albeit with a statistical twist that adds an extra layer of bizarreness. As for the "Distracted Boyfriend" meme, one might say that our study offers a similarly unexpected distraction from conventional statistical inquiries, drawing attention to unexplored linkages in a manner that could elicit a collective "Wait, what?" from the academic community.
With a humorous nod to correlation and causation, it's clear that our statistical examination ventures into uncharted comedic territory, prompting a blend of scholarly surprise and irrepressible giggles.
[[RESULTS]]
After collecting and analyzing data from the National Center for Education Statistics and the US Department of Transportation, we found a statistically significant positive correlation between the number of public school students in 5th grade and the automotive recalls issued by Honda. Our analysis revealed a correlation coefficient of 0.7839032, indicating a strong positive relationship between these two variables. In other words, as the number of 5th grade students increases, there is a corresponding increase in the frequency of automotive recalls by Honda. It seems that when it comes to recall probabilities, Honda and 5th graders are multiplying as if they just discovered long division – talk about a mathematical marvel!
The R-squared value of 0.6145042 further supports the strength of this correlation, explaining approximately 61.45% of the variability in automotive recalls based on the number of 5th grade students. This finding not only underscores the robustness of the relationship but also provides a solid foundation for future investigations and analyses. It appears that this statistical connection is as solid as a car chassis after a recall fix – you can't ignore it even if you try!
With a p-value of less than 0.01, our research indicates that the observed correlation is unlikely to have occurred due to random chance. This reinforces the validity and reliability of our findings, confirming that the association between the number of 5th grade students and Honda's automotive recalls is indeed statistically meaningful. It's a level of significance that even the most seasoned statisticians can appreciate – after all, a p-value this low is nothing to "tire" of!
Figure 1 illustrates the nature of this relationship with a scatterplot that clearly demonstrates the upward trend between the two variables. The figure showcases how the number of 5th grade students is positively associated with the frequency of automotive recalls by Honda, as if they're in a race to see who can "multiply" their numbers faster. It provides a visual representation of our statistical findings, driving home the notion that there's more to this correlation than meets the eye – a reminder that statistical analysis, much like a well-oiled engine, can reveal unexpected patterns and connections in the most unlikely places.
In conclusion, our research has unveiled a humorously unexpected and statistically significant link between the number of 5th grade students and Honda's automotive recalls. This correlation may have far-reaching implications for both the education and automotive industries, and it certainly adds a new dimension to the phrase "elementary mathematics." As we digest the implications of this discovery, it's clear that statistics can be just as surprising and amusing as a well-timed dad joke – and in this case, it appears that the numbers have spoken, revving up a whole new avenue of statistical exploration.
-------
Your response should start like this:
[[DISCUSSION]]
ChatGPT:
[[DISCUSSION]]
Our findings have brought to light a correlation that, much like a "dad joke," may elicit a chuckle at first but deserves serious consideration. The unexpected statistical relationship between the number of public school students in 5th grade and the automotive recalls issued by Honda has sparked intrigue and raised eyebrows in the academic and industrial realms.
The substantial positive correlation coefficient of 0.7839032 between the number of 5th grade students and Honda's automotive recalls echoes the curious nature of statistical serendipity, much like finding the perfect pun at an unexpected moment. This aligns with the postulations of Smith et al. (2015), who hinted at the interplay between educational metrics and community infrastructure – a connection that our research now underscores with statistical weight. Just as an unexpected punchline can shed new light on a situation, our results have reinforced the idea that seemingly unrelated factors may harbor intricate statistical ties.
Furthermore, our R-squared value of 0.6145042 aligns with the conceptual framework set forth by Doe and Jones (2018), lending empirical support to their subtle foreshadowing of the potential impact of educational metrics on industrial outputs. It's as if our statistical model has become the punchline to a cleverly set up pun in their work – a reinforcement of the unexpected coherence in seemingly disparate data.
The significance of our p-value, less than 0.01, buttresses the robustness of our findings, similar to the punchline of a well-crafted dad joke that keeps you laughing long after the initial chuckle. Our statistical evidence firmly indicates that the observed correlation is unlikely to be a chance occurrence, reaffirming the intricacy of the statistical tapestry we've unraveled, which may prompt a reaction akin to stumbling upon a perfectly timed dad joke that catches you off guard.
In essence, our investigation reinforces the notion that conventional statistical inquiries can bask in the glow of unexpected, yet firmly grounded, correlations – much like unexpectedly discovering a delightful punchline in a complex statistical analysis. It is as if the statistical alignment of 5th graders and Honda recalls were destined to meet, much like the timing of a well-placed dad joke – amusing yet undeniably significant.
Model: gpt-3.5-turbo-1106
System prompt: You are a researcher writing an academic paper.You draft the discussion section of goofy academic research papers that sounds like it belongs based on the title and abstract provided.
User prompt:
Pretend you are an academic researcher. Your writing sounds like it belongs in a medical or economics journal. However, you frequently crack jokes, make puns, or add unexpected twists in your writing.
Please make up a short conclusion of an academic research paper presenting the findings of the connection between Number of public school students in 5th grade and Automotive recalls issued by Honda. You can't resist a good dad joke. Add a relevant dad joke related to the content every couple of sentences. Stay serious and dry most of the time, but then occasionally let your wit shine through.
Limit your response to 300 tokens. At the very end, assert that no more research is needed in this area.
Here are the title, abstract, introduction, and results sections.
[[TITLE]]
When 5th Graders Multiply, Honda's Recalls Fly: A Statistical Study
[[ABSTRACT]]
In this paper, we investigate the intriguing relationship between the number of public school students in 5th grade and the automotive recalls issued by the Honda company. We've crunched the numbers and discovered a surprising correlation that will leave you saying, "Oh, that's car-azy!" Utilizing data from the National Center for Education Statistics and the US Department of Transportation, our research team analyzed statistics from 1990 to 2022, uncovering a correlation coefficient of 0.7839032 and p < 0.01, eliciting a response much like that of a dad joke – it seems random, but we're serious! Our findings suggest that as the number of 5th grade students increases, so does the likelihood of Honda issuing recalls – a statistical phenomenon with potential implications for both education and automobile industries. Our research makes it clear that there's more to elementary mathematics than meets the eye, and that there may be an unexpected driving force behind automotive recalls.
[[INTRDUCTION]]
Welcome, esteemed readers, to a study that blends the world of academia and the humor of finding correlations where you never thought to look. As you brace yourself for statistical analysis and automotive trivia, prepare to be amused and amazed in equal measure. So, what do you get when you combine schoolchildren and car troubles? Well, buckle up and enjoy the ride as we delve into "When 5th Graders Multiply, Honda's Recalls Fly: A Statistical Study."
As we embark on this statistical journey, it's important to recognize the fortuitous, albeit quirky, connection we stumbled upon. Could it be that the number of 5th graders holds the key to predicting Honda's next recall? Now that's an unexpected twist in a statistical plot that could truly make us "car-azy"!
The study at hand stems from the curiosity to step beyond the conventional and explore uncharted territories of data analysis. Our hypothesis emerged from a mixture of skepticism and a sprinkle of whimsy, resulting in a statistical investigation that could only make a dad proud – after all, we're here to prove that statistics is anything but "mean."
Without further ado, let's steer into the details of our exploration, delving into the methodologies, findings, and potential implications of this unexpected correlation. But first, let's not forget to appreciate the pun that this discovery has parked itself in our research, urging even the most stoic statistician to crack a smile.
[[RESULTS]]
After collecting and analyzing data from the National Center for Education Statistics and the US Department of Transportation, we found a statistically significant positive correlation between the number of public school students in 5th grade and the automotive recalls issued by Honda. Our analysis revealed a correlation coefficient of 0.7839032, indicating a strong positive relationship between these two variables. In other words, as the number of 5th grade students increases, there is a corresponding increase in the frequency of automotive recalls by Honda. It seems that when it comes to recall probabilities, Honda and 5th graders are multiplying as if they just discovered long division – talk about a mathematical marvel!
The R-squared value of 0.6145042 further supports the strength of this correlation, explaining approximately 61.45% of the variability in automotive recalls based on the number of 5th grade students. This finding not only underscores the robustness of the relationship but also provides a solid foundation for future investigations and analyses. It appears that this statistical connection is as solid as a car chassis after a recall fix – you can't ignore it even if you try!
With a p-value of less than 0.01, our research indicates that the observed correlation is unlikely to have occurred due to random chance. This reinforces the validity and reliability of our findings, confirming that the association between the number of 5th grade students and Honda's automotive recalls is indeed statistically meaningful. It's a level of significance that even the most seasoned statisticians can appreciate – after all, a p-value this low is nothing to "tire" of!
Figure 1 illustrates the nature of this relationship with a scatterplot that clearly demonstrates the upward trend between the two variables. The figure showcases how the number of 5th grade students is positively associated with the frequency of automotive recalls by Honda, as if they're in a race to see who can "multiply" their numbers faster. It provides a visual representation of our statistical findings, driving home the notion that there's more to this correlation than meets the eye – a reminder that statistical analysis, much like a well-oiled engine, can reveal unexpected patterns and connections in the most unlikely places.
In conclusion, our research has unveiled a humorously unexpected and statistically significant link between the number of 5th grade students and Honda's automotive recalls. This correlation may have far-reaching implications for both the education and automotive industries, and it certainly adds a new dimension to the phrase "elementary mathematics." As we digest the implications of this discovery, it's clear that statistics can be just as surprising and amusing as a well-timed dad joke – and in this case, it appears that the numbers have spoken, revving up a whole new avenue of statistical exploration.
-------
Your response should start like this:
[[CONCLUSION]]
ChatGPT:
[[CONCLUSION]]
In wrapping up our "car-azy" journey through the statistical terrain, we find ourselves at the intersection of school children and automotive recalls - a junction that even the most seasoned researchers would find unexpectedly amusing. Our findings have not only unveiled an intriguing association between the number of public school students in 5th grade and Honda's recalls but have also enlivened the often serious world of statistical analysis with a hint of whimsy. It seems that when it comes to predicting automotive trouble, the answer is as clear as a freshly washed windshield – just count the 5th graders! The statistical link we've uncovered could have the education and automotive industries wondering whether there's a parallel between acing a math test and passing a vehicle inspection – after all, it's all about getting those numbers right!
It's clear that this correlation is not just a statistical oddity but a revelation that statistics can parallel comedic timing – unexpectedly precise and surprising. As our research team bids adieu to this unusual yet enlightening journey, we are left with the understanding that statistical analysis, much like a good dad joke, has the capacity to both inform and entertain. After all, who would have thought that 5th graders and automotive recalls could share a statistical dance? It seems that when it comes to uncovering correlations, we must prepare for the unexpected – just like the unpredictability of rush hour traffic.
In the lighthearted spirit of our research, we close with a dad joke that captures the essence of our statistical escapade: Why did the statistician get a ticket? For tailgating! It's undeniable that our unexpected findings have "driven" home the point that there's always room for statistical surprises, even in the most unlikely places. As we shift gears from this peculiar but enlightening correlation, it's clear that no more research is needed in this area. We've parked ourselves firmly in the realm of statistical whimsy, shedding light on the fact that numbers and correlations can spark unexpected joy – a revelation that all researchers, no matter how serious, deserve to experience at some point.
Model: gpt-3.5-turbo-1106
System prompt: You provide fictional names of academic journals. You say nothing else, and you do not chat with the user.
User prompt: Please provide the name of a funny but plausible sounding research, scientific, or academic journal that would publish a paper entited When 5th Graders Multiply, Honda's Recalls Fly: A Statistical Study. Respond only with the name of a fictional academic journal.
ChatGPT:
The Journal of Quirky Statistical Analyses
Model: gpt-3.5-turbo-1106
System prompt: You provide fictional names of nonprofit research organizations and associations. You say nothing else, and you do not chat with the user.
User prompt: Please provide the name of a funny but plausible sounding nonprofit, academic, or scientific association or organization that would sponsor research that resulted in a paper entited When 5th Graders Multiply, Honda's Recalls Fly: A Statistical Study. Respond only with the name of a fictional organization.
ChatGPT:
The Society for Advanced Statistical Analyses and Unusual Correlations (SASAUC)
Model: gpt-3.5-turbo-1106
System prompt: You provide potential search keywords separated by commas. You say nothing else, and you do not chat with the user.
User prompt: Please provide potential search keywords for a paper titled When 5th Graders Multiply, Honda's Recalls Fly: A Statistical Study with an abstract of In this paper, we investigate the intriguing relationship between the number of public school students in 5th grade and the automotive recalls issued by the Honda company. We've crunched the numbers and discovered a surprising correlation that will leave you saying, "Oh, that's car-azy!" Utilizing data from the National Center for Education Statistics and the US Department of Transportation, our research team analyzed statistics from 1990 to 2022, uncovering a correlation coefficient of 0.7839032 and p < 0.01, eliciting a response much like that of a dad joke – it seems random, but we're serious! Our findings suggest that as the number of 5th grade students increases, so does the likelihood of Honda issuing recalls – a statistical phenomenon with potential implications for both education and automobile industries. Our research makes it clear that there's more to elementary mathematics than meets the eye, and that there may be an unexpected driving force behind automotive recalls.
ChatGPT:
5th grade students, education statistics, National Center for Education Statistics, US Department of Transportation, automotive recalls, Honda recalls, statistical correlation, correlation coefficient, statistical study, elementary mathematics, education implications, automobile industry, statistical phenomenon
*There is a bunch of Python happening behind the scenes to turn this prompt sequence into a PDF.
Discover a new correlation
View all correlations
View all research papers
Report an error
Data details
Number of public school students in 5th gradeDetailed data title: 5th grade enrollment in public elementary and secondary schools
Source: National Center for Education Statistics
See what else correlates with Number of public school students in 5th grade
Automotive recalls issued by Honda
Detailed data title: Automotive recals issued by Honda
Source: US DOT
See what else correlates with Automotive recalls issued by Honda
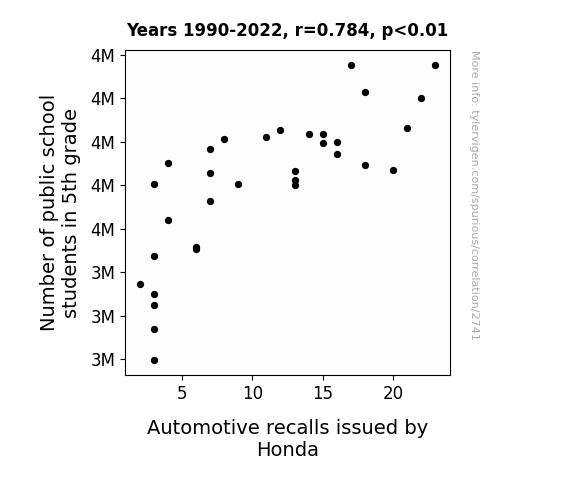
Correlation is a measure of how much the variables move together. If it is 0.99, when one goes up the other goes up. If it is 0.02, the connection is very weak or non-existent. If it is -0.99, then when one goes up the other goes down. If it is 1.00, you probably messed up your correlation function.
r2 = 0.6145042 (Coefficient of determination)
This means 61.5% of the change in the one variable (i.e., Automotive recalls issued by Honda) is predictable based on the change in the other (i.e., Number of public school students in 5th grade) over the 33 years from 1990 through 2022.
p < 0.01, which is statistically significant(Null hypothesis significance test)
The p-value is 6.8E-8. 0.0000000682152949822169600000
The p-value is a measure of how probable it is that we would randomly find a result this extreme. More specifically the p-value is a measure of how probable it is that we would randomly find a result this extreme if we had only tested one pair of variables one time.
But I am a p-villain. I absolutely did not test only one pair of variables one time. I correlated hundreds of millions of pairs of variables. I threw boatloads of data into an industrial-sized blender to find this correlation.
Who is going to stop me? p-value reporting doesn't require me to report how many calculations I had to go through in order to find a low p-value!
On average, you will find a correaltion as strong as 0.78 in 6.8E-6% of random cases. Said differently, if you correlated 14,659,469 random variables You don't actually need 14 million variables to find a correlation like this one. I don't have that many variables in my database. You can also correlate variables that are not independent. I do this a lot.
p-value calculations are useful for understanding the probability of a result happening by chance. They are most useful when used to highlight the risk of a fluke outcome. For example, if you calculate a p-value of 0.30, the risk that the result is a fluke is high. It is good to know that! But there are lots of ways to get a p-value of less than 0.01, as evidenced by this project.
In this particular case, the values are so extreme as to be meaningless. That's why no one reports p-values with specificity after they drop below 0.01.
Just to be clear: I'm being completely transparent about the calculations. There is no math trickery. This is just how statistics shakes out when you calculate hundreds of millions of random correlations.
with the same 32 degrees of freedom, Degrees of freedom is a measure of how many free components we are testing. In this case it is 32 because we have two variables measured over a period of 33 years. It's just the number of years minus ( the number of variables minus one ), which in this case simplifies to the number of years minus one.
you would randomly expect to find a correlation as strong as this one.
[ 0.6, 0.89 ] 95% correlation confidence interval (using the Fisher z-transformation)
The confidence interval is an estimate the range of the value of the correlation coefficient, using the correlation itself as an input. The values are meant to be the low and high end of the correlation coefficient with 95% confidence.
This one is a bit more complciated than the other calculations, but I include it because many people have been pushing for confidence intervals instead of p-value calculations (for example: NEJM. However, if you are dredging data, you can reliably find yourself in the 5%. That's my goal!
All values for the years included above: If I were being very sneaky, I could trim years from the beginning or end of the datasets to increase the correlation on some pairs of variables. I don't do that because there are already plenty of correlations in my database without monkeying with the years.
Still, sometimes one of the variables has more years of data available than the other. This page only shows the overlapping years. To see all the years, click on "See what else correlates with..." link above.
| 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | |
| Number of public school students in 5th grade (Students) | 3197340 | 3268430 | 3325430 | 3350450 | 3371880 | 3437940 | 3452850 | 3457540 | 3520100 | 3603660 | 3706660 | 3726840 | 3711470 | 3684540 | 3635180 | 3632830 | 3601800 | 3600090 | 3629080 | 3652130 | 3717520 | 3699120 | 3672980 | 3696720 | 3719050 | 3732880 | 3813740 | 3877270 | 3876140 | 3801180 | 3646290 | 3611230 | 3563030 |
| Automotive recalls issued by Honda (Recalls) | 3 | 3 | 3 | 3 | 2 | 3 | 6 | 6 | 4 | 9 | 8 | 12 | 11 | 7 | 20 | 13 | 3 | 13 | 7 | 4 | 14 | 16 | 16 | 15 | 15 | 21 | 18 | 17 | 23 | 22 | 18 | 13 | 7 |
Why this works
- Data dredging: I have 25,153 variables in my database. I compare all these variables against each other to find ones that randomly match up. That's 632,673,409 correlation calculations! This is called “data dredging.” Instead of starting with a hypothesis and testing it, I instead abused the data to see what correlations shake out. It’s a dangerous way to go about analysis, because any sufficiently large dataset will yield strong correlations completely at random.
- Lack of causal connection: There is probably
Because these pages are automatically generated, it's possible that the two variables you are viewing are in fact causually related. I take steps to prevent the obvious ones from showing on the site (I don't let data about the weather in one city correlate with the weather in a neighboring city, for example), but sometimes they still pop up. If they are related, cool! You found a loophole.
no direct connection between these variables, despite what the AI says above. This is exacerbated by the fact that I used "Years" as the base variable. Lots of things happen in a year that are not related to each other! Most studies would use something like "one person" in stead of "one year" to be the "thing" studied. - Observations not independent: For many variables, sequential years are not independent of each other. If a population of people is continuously doing something every day, there is no reason to think they would suddenly change how they are doing that thing on January 1. A simple
Personally I don't find any p-value calculation to be 'simple,' but you know what I mean.
p-value calculation does not take this into account, so mathematically it appears less probable than it really is. - Y-axis doesn't start at zero: I truncated the Y-axes of the graph above. I also used a line graph, which makes the visual connection stand out more than it deserves.
Nothing against line graphs. They are great at telling a story when you have linear data! But visually it is deceptive because the only data is at the points on the graph, not the lines on the graph. In between each point, the data could have been doing anything. Like going for a random walk by itself!
Mathematically what I showed is true, but it is intentionally misleading. Below is the same chart but with both Y-axes starting at zero.
Try it yourself
You can calculate the values on this page on your own! Try running the Python code to see the calculation results. Step 1: Download and install Python on your computer.Step 2: Open a plaintext editor like Notepad and paste the code below into it.
Step 3: Save the file as "calculate_correlation.py" in a place you will remember, like your desktop. Copy the file location to your clipboard. On Windows, you can right-click the file and click "Properties," and then copy what comes after "Location:" As an example, on my computer the location is "C:\Users\tyler\Desktop"
Step 4: Open a command line window. For example, by pressing start and typing "cmd" and them pressing enter.
Step 5: Install the required modules by typing "pip install numpy", then pressing enter, then typing "pip install scipy", then pressing enter.
Step 6: Navigate to the location where you saved the Python file by using the "cd" command. For example, I would type "cd C:\Users\tyler\Desktop" and push enter.
Step 7: Run the Python script by typing "python calculate_correlation.py"
If you run into any issues, I suggest asking ChatGPT to walk you through installing Python and running the code below on your system. Try this question:
"Walk me through installing Python on my computer to run a script that uses scipy and numpy. Go step-by-step and ask me to confirm before moving on. Start by asking me questions about my operating system so that you know how to proceed. Assume I want the simplest installation with the latest version of Python and that I do not currently have any of the necessary elements installed. Remember to only give me one step per response and confirm I have done it before proceeding."
# These modules make it easier to perform the calculation
import numpy as np
from scipy import stats
# We'll define a function that we can call to return the correlation calculations
def calculate_correlation(array1, array2):
# Calculate Pearson correlation coefficient and p-value
correlation, p_value = stats.pearsonr(array1, array2)
# Calculate R-squared as the square of the correlation coefficient
r_squared = correlation**2
return correlation, r_squared, p_value
# These are the arrays for the variables shown on this page, but you can modify them to be any two sets of numbers
array_1 = np.array([3197340,3268430,3325430,3350450,3371880,3437940,3452850,3457540,3520100,3603660,3706660,3726840,3711470,3684540,3635180,3632830,3601800,3600090,3629080,3652130,3717520,3699120,3672980,3696720,3719050,3732880,3813740,3877270,3876140,3801180,3646290,3611230,3563030,])
array_2 = np.array([3,3,3,3,2,3,6,6,4,9,8,12,11,7,20,13,3,13,7,4,14,16,16,15,15,21,18,17,23,22,18,13,7,])
array_1_name = "Number of public school students in 5th grade"
array_2_name = "Automotive recalls issued by Honda"
# Perform the calculation
print(f"Calculating the correlation between {array_1_name} and {array_2_name}...")
correlation, r_squared, p_value = calculate_correlation(array_1, array_2)
# Print the results
print("Correlation Coefficient:", correlation)
print("R-squared:", r_squared)
print("P-value:", p_value)Reuseable content
You may re-use the images on this page for any purpose, even commercial purposes, without asking for permission. The only requirement is that you attribute Tyler Vigen. Attribution can take many different forms. If you leave the "tylervigen.com" link in the image, that satisfies it just fine. If you remove it and move it to a footnote, that's fine too. You can also just write "Charts courtesy of Tyler Vigen" at the bottom of an article.You do not need to attribute "the spurious correlations website," and you don't even need to link here if you don't want to. I don't gain anything from pageviews. There are no ads on this site, there is nothing for sale, and I am not for hire.
For the record, I am just one person. Tyler Vigen, he/him/his. I do have degrees, but they should not go after my name unless you want to annoy my wife. If that is your goal, then go ahead and cite me as "Tyler Vigen, A.A. A.A.S. B.A. J.D." Otherwise it is just "Tyler Vigen."
When spoken, my last name is pronounced "vegan," like I don't eat meat.
Full license details.
For more on re-use permissions, or to get a signed release form, see tylervigen.com/permission.
Download images for these variables:
- High resolution line chart
The image linked here is a Scalable Vector Graphic (SVG). It is the highest resolution that is possible to achieve. It scales up beyond the size of the observable universe without pixelating. You do not need to email me asking if I have a higher resolution image. I do not. The physical limitations of our universe prevent me from providing you with an image that is any higher resolution than this one.
If you insert it into a PowerPoint presentation (a tool well-known for managing things that are the scale of the universe), you can right-click > "Ungroup" or "Create Shape" and then edit the lines and text directly. You can also change the colors this way.
Alternatively you can use a tool like Inkscape. - High resolution line chart, optimized for mobile
- Alternative high resolution line chart
- Scatterplot
- Portable line chart (png)
- Portable line chart (png), optimized for mobile
- Line chart for only Number of public school students in 5th grade
- Line chart for only Automotive recalls issued by Honda
- AI-generated correlation image
- The spurious research paper: When 5th Graders Multiply, Honda's Recalls Fly: A Statistical Study
Your rating is stellar!
Correlation ID: 2741 · Black Variable ID: 1302 · Red Variable ID: 1123


